Physique

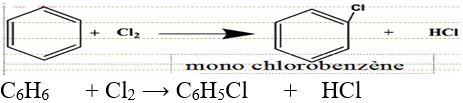
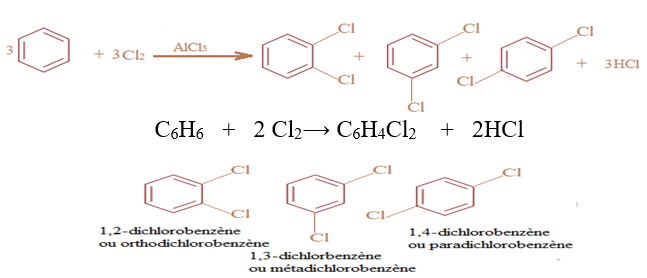
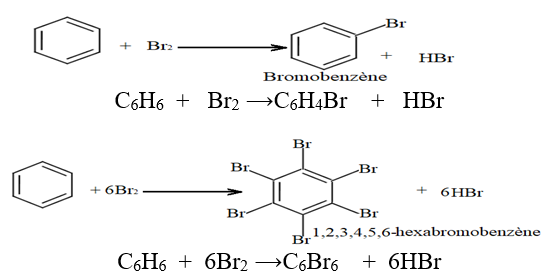
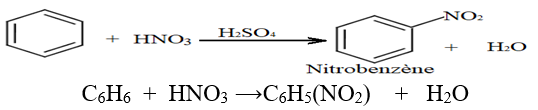Les composés oxygénés - 1er s

Classe: 
Première
 
 
Un composé organique oxygéné est un corps pur organique dont la molécule comporte les éléments carbone, oxygène et hydrogène 
 
Un groupement d'atomes de carbone, oxygène et hydrogène d'une molécule qui sont agencés d'une certaine façon et qui ont des propriétés identifiables. 
 
On étudiera dans ce chapitre les fonctions alcool, aldéhyde, cétone, acide carboxylique et ester

I. Présentation des composés oxygénés

1. L'atome d'oxygène

L'oxygène a pour numéro atomique $Z=8$ et sa structure électronique $(K)^{2}(L)^{6}$
 
Son schéma de Lewis est : 
 
L'atome d'oxygène peut donc établir soit deux liaisons simples, soit une double liaison

2. Les liaisons de covalence établies par les atomes d'oxygène

Avec le carbone et l'hydrogène, les types d'enchainements possibles sont :
 
 
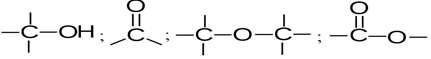
Chacun des groupements ainsi constitués confèrent aux molécules qui le contiennent un ensemble de propriétés. 
 
On définit alors une fonction et le groupement constitué porte le nom groupe fonctionnel

II. Composés dont la molécule comporte un atome d'oxygène 

1. Les alcools et les éthers-oxydes

Ce sont des composés organiques oxygénés comportant un seul un atome d'oxygène 
 
Leur formule brute générale est : $C_{n}H_{2n+2}O_{2}$

1.1 Les alcools 

1.1.1 Définition

Les alcools sont des composés organiques oxygénés comportant le groupe fonctionnel hydroxyle $(-OH)$ lié à un carbone tétragonal appelé carbone fonctionnel
 
La formule générale d'un alcool est : $R-OH\text{ ou }C_{n}H_{2n+1}OH$

1.1.2 Les classes d'alcools 

Un alcool est dit primaire, secondaire ou tertiaire selon que le carbone du groupe fonctionnel $($atome de carbone lié au groupe $–OH)$ est lié respectivement à un zéro ou un atome ; deux atomes ; ou trois atomes  de carbone
 
 

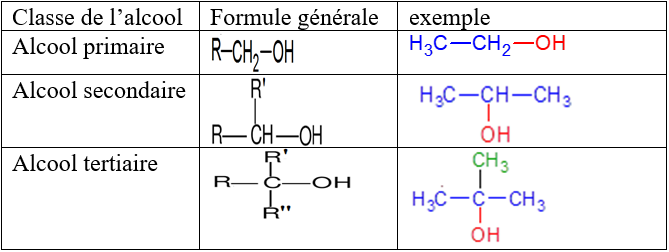
Remarque

$R$, $R'$ et $R''$ sont des groupes alkyles

1.1.3 Nomenclature

Le nom d'un alcool dérive de celui de l'alcane correspondant en remplace le $« e »$ final de l'alcane par la terminaison $« ol »$, précédée, si nécessaire, de l'indice de position du groupe hydroxyle dans la chaîne carbonée principale.

Exemples

$\text{Butan}-2-ol\qquad\qquad 5-\text{méthylhexan}-3-ol$

1.2 Les éthers-oxydes

1.1.1 Définition 

Un éther-oxyde est un composé organique oxygéné contenant un atome d'oxygène lié à deux atomes de carbone à structure tétraédrique
 
La formule générale d'un éther-oxyde est : $R-O-R’’$ où $R$ et $R’’$ sont des groupes alkyles

1.1.2 Nomenclature

Pour un éther-oxyde, on considère le plus petit groupe $(R$ par exemple$)$ pour former le substituant alcoxy et on nomme le composé comme substituant de l'autre $R’$ de la molécule

Exemples 

$CH_{3}-CH_{2}-O-CH3$ : Méthoxyéthane ou oxyde d'éthyle et de méthyle,
 
$CH_{3}-CH(CH_{3})-O-CH_{3}$ : Méthoxyméthyl $-2-$ propane ou oxyde de méthyle et de $2-$ propyle.
 
$CH_{3}-CH(CH_{3})-CH_{2}-O-CH_{3}$ : méthoxy $-2-$ méthylpropane ou oxyde de méthyle et de $(2-$ méthyl$)$ propyle.

1.1.3 Quelques propriétés des éthers-oxydes

Les éthers-oxydes sont pour la plus plupart à l'état liquide
 
A température ordinaire, ils sont beaucoup plus volatils et beaucoup moins solubles dans l'eau

2. Les aldéhydes et les cétones 

Les aldéhydes et les cétones sont des composés carbonylés de formule brute générale $C_{n}H_{2n}O$
 
Un dérivé carbonylé est un composé organique oxygéné qui comporte le groupe carbonyle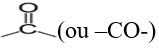 
 
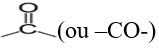
Le carbone doublement lié à l'oxygène peut être lié à un ou (des atomes) de carbone ou un atome d'hydrogène
 
L'atome de carbone du groupement carbonyle est appelé carbone fonctionnel.
 
Il est trigonal

2.1 Les aldéhydes

2.1.1 Définition 

Un aldéhyde est un composé organique oxygénée qui contient le groupe caractéristique 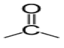, appelé groupe carbonyle, directement lié à au moins un atome d'hydrogène :
 
Les aldéhydes ont pour formule générale :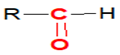 
 
où $R$ est un groupe alkyle 

Remarques :

$-\ $ Dans un aldéhyde, le groupe carbonyle est toujours situé à l'extrémité de la chaîne carbonée 
 
$-\ $ La formule semi-développée générale d'un aldéhyde peut s'écrire : $RCHO$ ou $R‒CHO$

Exemples

 
 

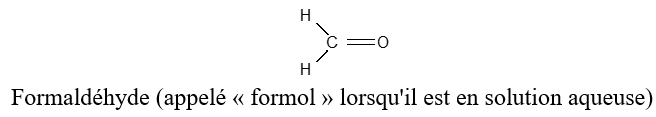
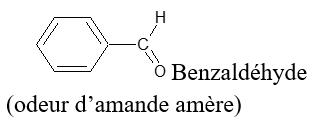
2.1.2 Nomenclature

Le nom d'un aldéhyde dérive de celui de l'alcane correspondant en remplaçant le $« e »$ final de l'alcane par la terminaison $« al ».$

Exemples

 
 

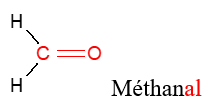
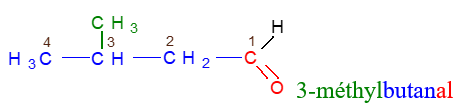
2.2 Les cétones

2.2.1 Définition

Une cétone est un composé organique oxygénée qui contient le groupe carbonyle $-C=O$, directement lié à deux atomes de carbone
 
La formule générale est : 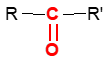 où $R$ et $R'$ sont des groupes alkyles

Remarques 

$-\ $ Dans une cétone, le groupe carbonyle ne peut pas être situé à l'extrémité de la chaîne carbonée, contrairement à un aldéhyde ;
 
$-\ $ La formule semi-développée générale d'une cétone peut s'écrire : $RCOR’$ ou $R‒CO‒R’.$

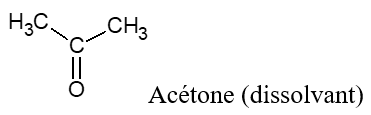
Exemples 

 

2.2.2 Nomenclature

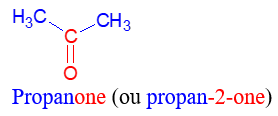
Le nom d'une cétone dérive de celui de l'alcane correspondant en remplaçant le $« e »$ final de l'alcane par la terminaison $« one »$, précédée, si nécessaire, de l'indice de position du groupe carbonyle dans la chaîne carbonée principale

Exemples 

 
 

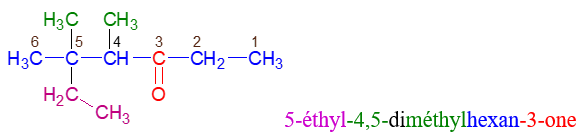
2.3 Tests des aldéhydes et des cétones

Pour repérer la présence d'un aldéhyde ou d'une cétone dans un milieu réactionnel, il est possible d'utiliser des tests d'identification : l'ajout d'un réactif particulier provoque la formation d'un précipité ou un changement de couleur du milieu
 
 

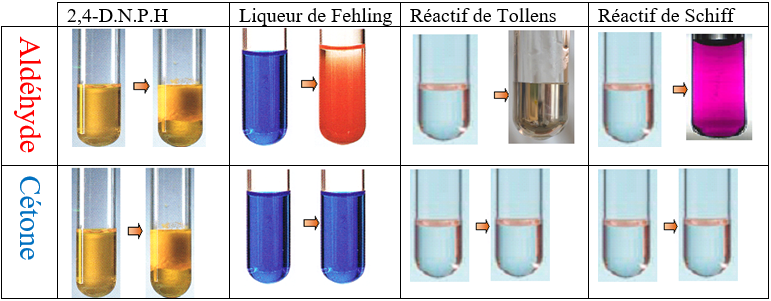
$\bullet $ Test à la $D.N.P.H.$

La $D.N.P.H.$ $(2.4-$ dinitrophénylhydrazine$)$ réagit en présence du groupe  carbonyle $─CO─$ et donne un précipité jaune. 
 
La $D.N.P.H.$ réagit avec les cétones et les aldéhydes 

$\bullet $ Test à la liqueur de Fehling 

La liqueur de Fehling est obtenue en mélangeant une solution aqueuse acidifiée de sulfate de cuivre $(CuSO_{4}\;,\ 5H_{2}O)$ et une solution aqueuse basique de tartrate de sodium et de potassium $(KNaC_{4}H_{4}O_{6}\;,\ 4H_{2}O).$ 
 
Elle contient des ions cuivre $(II)Cu^{2+}$ (de couleur bleue en solution aqueuse).
 
A chaud, en milieu basique, l'aldéhyde réduit les ions $Cu^{2+}$ en oxyde de cuivre $I(Cu_{2}O_{(s)})$ qui forme un précipité rouge brique.
 
L'équation de la réaction (d'oxydoréduction) est la suivante :
 
$R-CHO+2Cu^{2+}+5HO^{-}\rightarrow R-COO^{-}+Cu_{2}O+3H_{2}O$

$\bullet $ Test de Tollens

Le réactif de Tollens est une solution de nitrate d'argent en milieu ammoniacal : elle est obtenue en mélangeant une solution aqueuse de nitrate d'argent $($ à $5\%)$ avec une solution concentrée d'ammoniaque.
 
Elle contient des ions argent $Ag^{+}$ (incolores).
 
En milieu basique, les ions $Ag^{+}$ sont réduits par l'aldéhyde et forment un dépôt d'argent solide (« miroir d'argent ») selon la réaction suivant :
$$R-CHO+2Ag^{+}+3HO^{-}\rightarrow\;R-COO^{-}+2Ag+2H_{2}O$$ 

$\bullet $ Test au réactif de Schiff 

Les aldéhydes peuvent être facilement mis en évidence par le réactif de Schiff.
 
Un papier filtre imbibé de réactif de Schiff rosit dès qu'il entre en contact avec des vapeurs d'un aldéhyde (très volatile).
 
Dès qu'on verse quelques gouttes d'éthanal dans le réactif de Schiff, celui-ci se colore en rose.

Remarques

$-\ $ La $D.N.P.H.$ est commun aux aldéhydes et aux cétones.
 
$-\ $ La liqueur de Fehling, le réactif de Tollens et le réactif de Schiff  sont aux aldéhydes

II. Composés dont la molécule comporte deux atomes d'oxygène 

Les acides carboxyliques et les esters sont des composés organiques oxygénés de formule brute générale $C_{n}H_{2n}O_{2}$ 

1. Les acides carboxyliques 

1.1 Définition

Un acide carboxylique est un composé organique oxygéné qui contient le groupe carboxyle  $«‒COOH »$ ou 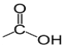 directement lié à un atome de carbone 
 
La formule générale d'un acide carboxylique est :
 
 

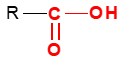
Remarques :

$-\ $ Dans un acide carboxylique, le groupe carboxyle est toujours situé à l'extrémité de la chaîne carbonée ;
 
$-\ $ La formule semi-développée générale d'un acide carboxylique s'écrire : $RCOOH$ ou $R‒COOH$ ou $RCO_{2}H$

Exemple :

 

1.2 Nomenclature

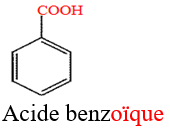
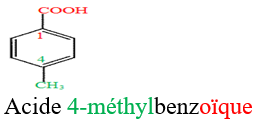
Le nom d'un acide carboxylique dérive de celui de l'alcane correspondant en remplaçant le $« e »$ final de l'alcane par la terminaison $« oïque »$ et le tout précédé par le mot $« acide ».$

Exemples :

$HCOOH$ Acide méthanoïque (ou acide formique)
 
$CH_{3}-COOH$ Acide méthanoïque (ou acide acétique)
 
$HOOC-COOH$ Acide éthanedioïque (ou acide oxalique)
 
 
 
 
 

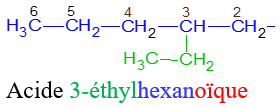
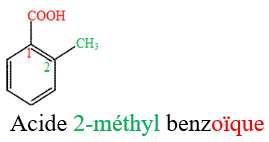
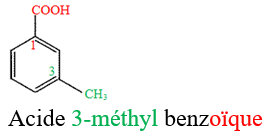
1.3 Test d'identification des acides carboxyliques

Les acides carboxyliques sont caractérisés par la présence du groupe carboxyle $–COOH$ dans leur molécule.
 
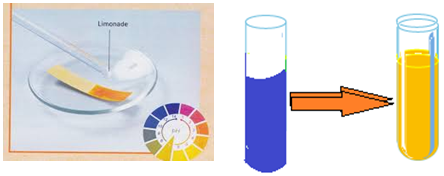
Un acide carboxylique provoque la décoloration du papier $pH$ (teinte acide)
 
Il provoque aussi le passage de la teinte verte à la teinte jaune pour le bleu de bromothymol $(BBT)$ 
 
 

Remarque :

Le groupe hydroxyle $(–OH)$ du groupement carboxyle n'est pas un groupe hydroxyle car il est lié à un atome de carbone, lui-même lié par une liaison covalente double à un atome d'oxygène.

2. Les esters 

2.1 Définition

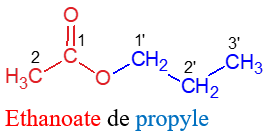
Un ester est un composé organique oxygéné qui possède le groupe fonctionnel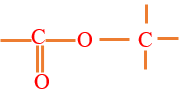 
 
La formule générale d'un ester est :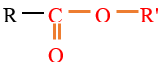 

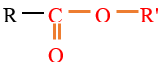
2.2 Nomenclature

Le nom de l'ester s'obtient  en faisant suivre le nom du groupe  carboxylate  de celui du groupe alkyle $-R$

Exemples

 

2.3 Test de reconnaissance des esters


 
Auteur: 
Sidy Mouhamed Ndiaye

Le composés aromatiques : le benzène - 1er s

Classe: 
Première
 

I. Structure 

1. Exemple du Benzène

Le benzène est un hydrocarbure instauré liquide, incolore non miscible dans l'eau. 
 
La formule brute est $C_{6}$ $H_{6}.$ 
 
L'étude expérimentale de la molécule par des méthodes physiques montre que la molécule est plane et cyclique. 
 
Les six  atomes de carbones occupent chacun le sommet d'un hexagone (six côtés, six sommets). 
 
La longueur de liaisons $(C\ –\ C)$ de la molécule de benzène est intermédiaire entre celle d'une liaison et celle d'une liaison double. 
 
Les longueurs de liaisons $(C\ -\ C)$ sont identiques $d_{c-c}=140\,pm$
 
$$d(C=C)\ <\ d(C-C)\ <\ d(C-C)$$
$$\text{Alcène}\;(134\,pm)\ \text{Benzène}\;(140\,pm)\ \text{Alcane}\;(154\,pm)$$
 
 

$\bullet $ Géométrie de la molécule

Les six électrons disponibles forment le nuage électronique en faisant une liaison collective entre (sextet) les six atomes de carbone. 
 
L'ensemble des six atomes ainsi liés et appelé noyau benzénique » ou encore appelé « noyau aromatique »
 
 

2. Exemple d'autres composés aromatiques

On appel composé aromatiques tout composé comportant d'un ou plusieurs noyaux benzéniques confèrent à la molécule des propriétés particuliers.
 
Il n'existe pas de nomenclature systématique.
 
On les nomme en générale comme des dérivés substitués du benzène. 
 
 

II. Propriétés du Benzène

1. Propriétés physiques du benzène

C'est un liquide incolore dans des conditions ordinaires de température et de pression. 
 
Il est caractérisé par une température de fusion de $5.5^{\circ}C$ et une température d'ébullition à $80^{\circ}C.$ 
 
Il est insoluble dans l'eau, c' est un bon solvant (il dissout les coups gras l'iode, le soufre...) et soluble dans  l'alcool et dans l'éther.

2. Propriétés chimiques

2.1. Réaction de combustion

Les réactions de combustion sont des réactions de destruction ; c'est-à-dire une réaction au cours de laquelle le squelette carboné de la molécule est complètement détruit.  
 
$C_{6}H_{6}+\dfrac{15}{2}\rightarrow 6CO_{2}+3H_{2}O$
 
ou $2C_{6}H_{6}+15O_{2}\rightarrow 12CO_{2}+6H_{2}O$
 
L'équation montre que la quantité de dioxygène (coefficients stœchiométriques) nécessite une quantité importante de dioxygène pour obtenir une combustion complète.

2.2. Réactions de substitution 

Une réaction de substitution sur le benzène consiste à remplacer un ou des atome(s) d'hydrogène par un atome ou un groupe d'atomes, tout en conservant le noyau benzénique.

2.2.1 Coloration du Benzène

Afin d'éviter une réaction d'addition, on opère à l'abri de la lumière. 
 
En présence d'un catalyseur, le chlorure d'aluminium, $AlCl_{3}$, le dichlore réagit avec le benzène suivant une réaction de substitution : 
 
$-\ $ Lorsque le dichlore n'est pas en excès, on obtient une mono substitution 
 
 
$-\ $ Lorsque le dichlore est en excès et que la réaction se poursuit, on obtient une di, tri, tétra, penta puis une hexasubstitution. 
 
La réaction de disubstitution fournit un mélange de trois isomères. 

Exemples

 

2.2.2 Bromation du Benzène

En l'absence de lumière la réaction se fait dans l'obscurité mais elle nécessite un catalyseur comme le bromure de fer $III$ $(FeBr_{3}).$ 
 
Si le dibrome est un excès on peut obtenir des dérives polysubstitués bromés du benzène.

Exemples

 

2.2.3 Nitration du Benzène

L'acide nitrique $HNO_{3}$ concentré réagit sur le benzène en présence de l'acide sulfurique comme catalyseur
 
L'équation de la réaction s'écrit :
 
 
A température élevée $(90^{\circ})$ il est possible d'obtenir le dinitrobenzène et du trinitrobenzène
 
 

2.2.4 Sulfonation du Benzène

La sulfonation  du benzène peut être effectuée en portant à reflux un mélange de benzène et d'oléum $(SO_{3}\;,\ H_{2}SO_{4})$
 
L'équation de la réaction s'écrit :
 
 

2.2.5 Alkylation

Il s'agit de greffer une chaine alkyle sur le cycle benzénique. 
 
On utilise $AlCl_{3}$ ou $AlBr_{3}$ comme catalyseur.

Exemple :

 

2.2.6 Alcoylation

Il s'agit d'une synthèse de cétone aromatique.
 
Le réactif alcylant  est un halogénure d'acyle ou en anhydride d'acide.
 
La réaction nécessite l'utilisation d'un catalyseur comme le chlorure d'aluminium $AlCl_{3}$ 

Exemple :

 

2.3 Réactions d'addiction

Elles sont difficiles à réaliser et s'effectuent en une seule étape et avec un changement de la structure de la molécule.

2.3.1 Hydrogénation

Elle nécessite la présence de catalyseur très réactif comme le nickel $(Ni)$, le platine $(Pt).$
 
 
La molécule ne présente plus son caractère aromatique (destruction du noyau benzénique), on passe de la configuration à plusieurs conformations dont celle du bateau et chaise.
 

2.3.2 Addition du dichlore

L'addition du dichlore sur le benzène est une réaction photochimique (présence de lumière) on obtient l'hexachlorohexane. 
 
Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Réflexion de la lumière - 2nd S

Classe: 
Seconde
 

Exercice 1

1) Qu'est-ce que la réflexion ?
 
2) Qu'est-ce qu'une surface réfléchissante ?
 
Donner des exemples de surfaces réfléchissantes.
 
3) Qu'est-ce qu'un dioptre ? Donner des exemples de dioptres.
 
4) Qu'est-ce qu'un dioptre plan ? Donner des exemples de dioptres plans
 

Exercice 2

1) Énoncer les lois de Descartes relatives à la réflexion de la lumière.

 

 
Un miroir plan $M$ est placé horizontalement. 
 
L'œil d'un observateur se trouve en $O$, à une distance de $1.5\;m$ au dessus du bord du miroir.
 
Un objet lumineux ponctuel S est situé au dessus du miroir.
 
L'observateur regarde le miroir et observe l'image de l'objet $S$ donnée par le miroir.
 
2.1) Expliquer pourquoi le miroir donne de l'objet $S$ une image.
 
Préciser la position de cette image.
 
2.2) Construire la marche du rayon lumineux issu de $S$ et qui, après réflexion sur le miroir arrive en $O.$
 
3) Le point S se déplace suivant une droite $\Delta$ parallèle au miroir et qui coupe la verticale $OH.$
 
Données :
 
$-\ $ distance de $S$ au miroir $1\;m$ ;
 
$-\ $ distance $OH=1.5\;m$ ;
 
$-\ $ longueur du miroir $2\;m.$
 
Déterminer les positions de $S$ pour lesquelles l'observateur peut voir l'image $S'\ $ de $\ S$ en regardant la face du miroir
 

Exercice 3

Le miroir $M_{1}M_{2}$ est placé dans le plan perpendiculaire à la figure et contenant les points : $M_{1}(0\;;\ -1.5)\ $ et $\ M_{2}(0\;;\ 3).$

 

 
L'œil de l'observateur est placé en $\Omega(3\;;\ 0).$
 
Placez les points $A(3\;;\ 3)$, $B(3\;;\ 6)\ $ et $\ C(1.5\;;\ 6).$
 
L'œil peut-il voir les images $A'\;,\ B'\ $ et $\ C'$ des points $A\;,\ B\ $ et $\ C\ ?$
 

Exercice 4

Un personnage de $1.8\;m$ se regarde dans un miroir vertical situé à $2\;m.$
 
La distance Yeux-sol est de $1.6\;m$
 
1) Faire un schéma des rayons issus de l'œil allant à ses pieds au sommet de sa tête.
 
2) En déduire la taille minimale du miroir permettant à l'homme de se voir intégralement
 
3) A quelle distance du sol le miroir doit-il être pour que la personne se voie entièrement.
 
4) Si l'on s'éloigne que se passe-t-il ?
 

Exercice 5

1) On considère une source lumineuse ponctuelle $S$ située dans l'espace objet selon le schéma suivant :

 

 
On appelle $O$ la projection orthogonale de $S$ sur le plan du miroir. 
 
Mesurer la distance $OS.$ Quelle devra être la distance $OS'\ ?$
 
2) Tracer l'image $S'\ $ de $\ S$ par le miroir. Est-elle réelle ou virtuelle ? Justifier.
 
3) Un observateur est situé au point $A.$ Il observe $S'$ l'image de $S$ par le plan du miroir.
 
Tracer le rayon lumineux issu de $S’$ arrivant sur $A$. Justifier.
 
4) On appelle $O'$ le point d'intersection entre le rayon $S'A$ et le plan du miroir. 
 
Placer le point $O'$ sur le schéma.
 
5) Tracer le rayon lumineux $SO’$. En déduire la marche de la lumière ici de la source $S$ allant vers l'observateur $A.$
 
6) Tracer la normale au plan du miroir en $O'.$
 
7) Vérifier sur votre tracé que la deuxième loi de Descartes sur la réflexion est vérifiée

Exercice 6

Un rayon lumineux monochromatique d'un faisceau laser pénètre dans l'une des fibres optiques d'un fibroscope.
 
Son angle d'incidence en $I$ sur la paroi de la fibre est égal à $60^{\circ}.$ 
 
L'angle d'incidence à partir duquel il y a réflexion totale à la surface du verre est égal à $42^{\circ}$

 

 
1) Que signifie monochromatique ? La lumière du Soleil est-elle monochromatique ?
 
2) Identifier l'angle d'incidence au point $I$ sur le schéma
 
3) Y a-t-il réflexion totale en $I$ ? Justifier en rédigeant une réponse.
 
4) Déterminer la valeur de l'angle de réfraction issu du rayon incident en $O.$
 

Exercice 7

Lors d'une ronde d'inspection, une gardienne $(G)$ pénètre dans une salle dont deux murs sont recouverts d'un grand miroir plan. Un voleur $(V)$ se trouve dans la pièce. 
 
Avec sa lampe de poche, la gardienne envoie un faisceau ayant un angle d'ouverture de $15^{\circ}$ dans la direction indiquée ci-dessous.
 
Le voleur sera-t-il éclairé par le faisceau de la lampe de poche ?

 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Propagation rectiligne de la lumière - 2nd S

Classe: 
Seconde
 

Exercice 1

Dans les exemples proposés, choisir quels sont les objets lumineux qui sont des sources primaires, et ceux qui sont des sources secondaires.
 
Donner les résultats sous forme d'un tableau.
 
Flamme de bougie, mur blanc, lune, soleil, vénus, étoile polaire, satellite Spot, atmosphère (le ciel), écran de télévision, écran de projection
 

Exercice 2

Compléter :
 
Les$\ldots\ldots$produisent la lumière qu'elles émettent. 
 
Les sources secondaires sont des objets lumineux$\ldots\ldots$par des sources primaires.
 
La lumière émise par les sources se propage$\ldots\ldots$, dans un milieu$\ldots\ldots$et homogène. 
 
On traduit ce type de propagation la construction de droites orientées appelées$\ldots\ldots$
 
Vocabulaire qui peut être employé
 
Rayon, transparent, source, éclairé, primaire, isotrope, rectiligne ment, inférieure, supérieure.
 

Exercice 3

a) La distance de la terre au soleil est environ de $150000000\;km.$ Combien de temps met la lumière à nous parvenir ?
 
b) Pour mesurer la distance de la terre à la lune, les astronomes émettent un faisceau laser vers un réflecteur que les astronautes ont placé sur la lune. 
 
Le temps mis par la lumière pour revenir à l'observatoire est à un moment de l'année de $2.6\;s$
 
Quelle est la distance de la terre à la lune ?
 

Exercice 4

1) Qu'est-ce qu'un milieu transparent ?
 
2) Qu'est-ce qu'un milieu homogène ?
 
3) Donner des exemples de milieux transparents et homogènes.
 
4) Comment la lumière se propage-t-elle dans un tel milieu ?
 

Exercice 5

Le personnage voit une fleur dans le jardin

 

 
Dessiner et orienter le parcours de la lumière afin de décrire au mieux ce phénomène
 

Exercice 6


 
L'ampoule $(A)$ est branchée, prévoir par quel trou, $T_{1}\;,\ T_{2}\;,\ T_{3}$ un observateur peut voir de la lumière.
 
Utiliser le modèle de l'optique élémentaire pour réaliser vos prévisions
 

Exercice 7

Parmi les hypothèses suivantes, choisir celle(s) qui est (sont) possible(s).
 
1) la vue arrive aux objets si la lumière les éclaire.
 
2) la lumière éclaire l'œil, rebondit vers les objets et retourne à l'œil.
 
3) si vous voyez vos pieds c'est qu'ils émettent de la lumière.
 
4) la lumière éclaire les objets et elle est renvoyée vers l'œil.
 
5) l'œil voit les objets quand la vue est suffisamment forte pour y arriver : la vue est d'autant plus forte que la lumière ambiante est importante
 

Exercice 8

On considère une source ponctuelle S , une petite sphère de rayon $r=2\;cm$ et un écran placé à la distance $D=2.0\;m$ de la source $S.$ 
 
La sphère est placée à la distance $d=0.5\;m$ de la source ponctuelle de telle façon que l'on puisse voir son ombre portée sur l'écran. La source $S$ et les centres de l'écran et de la sphère sont alignés.

 

 
1) Quelle est la nature géométrique de l'ombre portée sur l'écran ?
 
2) Évaluer les dimensions de cette ombre portée, ainsi que sa surface.
 
3) On remplace la sphère par un disque de même rayon, à quelles conditions peut-on obtenir sur l'écran la même ombre portée qu'avec la sphère ?
 

Exercice 9

Des réflecteurs ont été déposés à la surface de la Lune lors des différentes missions lunaires Apollo.
 
Depuis la Terre, on vise un réflecteur à l'aide d'un faisceau laser et on mesure la durée $t$ séparant l'émission de la réception.
 
Lors d'une expérience, on a trouvé : $t=2.51\;s$
 
1) Déterminer la distance entre les surfaces des deux astres.
 
2) En déduire la distance entre leurs centres.
 
Données : rayon de la Terre $R_{T}=6.40\;10^{3}\;km$, rayon de la Lune $R_{L}=1.74\;10^{3}\;km$
 

Exercice 10

À partir d'une boîte parallélépipédique, Julien construit une chambre noire.
 
Puis il place face au trou (noté $O$) de diamètre $d=1\;mm$ un filament lumineux rectiligne $AB$ de hauteur $10\;cm$ ($O'$ milieu de $AB$) et d'épaisseur négligeable.
 
Le filament est disposé parallèlement à la face translucide, sa distance au trou $O$ est $D=60\;cm.$

 

 
1) En considérant le trou $O$ ponctuel et en utilisant des rayons lumineux issus de $A\ $ et $\ B.$
 
Montrer que l'œil de Julien placé derrière la feuille translucide voit une reproduction du filament renversée sur la feuille (on parlera d'image $A’B’)$, puis déterminer la taille de l'image $A’B’$
 
2) Montrer sur un schéma en vue du dessus avec deux rayons issus de $O’$ que le diamètre du trou influe sur la netteté de l'image. 
 
Établir la relation qui lie la largeur $e$ de l'image à la distance $D$ et aux caractéristiques de la chambre noire $(l\ $ et $\ d)$ puis calculer $e$

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 

 

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Réfraction - Dispersion de la lumière - 2nd S

Classe: 
Seconde
 

Exercice 1

Trouver les mots manquants
 
1) La$\ldots\ldots$est le changement de direction subi par un rayon lumineux lorsqu'il passe d'un milieu transparent dans un autre.
 
2) Une lumière$\ldots\ldots$ne peut pas être décomposée par un prisme. 
 
Elle est caractérisée par sa$\ldots\ldots$dans le vide.
 
3) Les longueurs d'onde dans le vide des radiations visibles sont comprises entre $400\ $ et $\ 800\ldots\ldots$environ.
 
4) Vrai ou faux ?
 
4.1) L'angle entre un rayon incident et la surface de séparation est appelé angle d'incidence.
 
4.2) Un rayon lumineux passe de l'air à l'eau (angle d'incidence $i$, angle de réfraction $r).$ 
 
On appelle indice de réfraction de l'eau le rapport $n=\dfrac{\sin i}{\sin r}.$
 
La décomposition de la lumière par un prisme est un phénomène de diffusion
 

Exercice 2

Un faisceau lumineux voyage dans l'eau, d'indice de réfraction $n=1.33.$ 
 
Il arrive à la surface de l'eau avec un angle d'incidence $i$ et se réfracte dans l'air. 
 
L'angle de réfraction est noté $r.$
 
1) Faire un schéma faisant apparaître toutes les grandeurs utiles.
 
2) Calculer $r$ dans le cas où $i=40^{\circ}.$
 
3) Faire de même dans le cas où $i=50^{\circ}.$ Que se passe-t-il dans ce cas ?
 
4) Montrer qu'il existe un angle $i_{max}$ appelé "angle de réflexion totale" pour lequel il n'y a pas de rayon réfracté. 
 
Donner son expression en fonction de $n$ et calculer sa valeur dans le cas de l'eau
 

Exercice 3

La réfraction d'un faisceau laser rouge passant de l'air dans l'eau est schématisée ci-dessous.

 

 
Données : indice de réfraction de l'air : $n_{air}=1$ ; indice de réfraction de l'eau : $n_{eau}=1.33.$
 
1) Reproduire et compléter le schéma en indiquant le point d'incidence $I$, en dessinant la normale et en repérant les angles d'incidence $i_{r}$ et de réfraction $r.$
 
2) Rappeler la loi de Descartes relative aux angles en respectant les notations du texte.
 
3) Calculer la valeur de l'angle de réfraction d'un rayon lumineux d'incidence $i_{air}=50^{\circ}.$
 

Exercice 4

1) On dirige un pinceau de lumière monochromatique rouge vers un demi-disque contenant un liquide.

 

 
1.1) Quel est le rayon réfracté ?
 
1.2) Quelles sont les valeurs de l'angle d'incidence $i$ et de l'angle de réfraction $r\ ?$
 
1.3) En utilisant la loi de Descartes pour la réfraction, calculer l'indice de réfraction $n$ du liquide.
 
L'indice de réfraction de l'air est égal à $1.$
 
2) On dirige un faisceau de lumière blanche vers un prisme.
 
2.1) Dessiner ce que l'on observe sur un écran placé derrière le prisme.

 

 
2.2) Quelle propriété du prisme est ainsi mise en évidence ?
 
2.3) De quelle grandeur $d$
 

Exercice 5

1) Un rayon lumineux passe du verre dans l'air (figure ci-dessous).

 

 
Comment appelle-t-on ?
 
a) le rayon $AO$ ;
 
b) le rayon $OB$ ;
 
c) l'angle $i_{1}$ ;
 
d) l'angle $i_{2}$
 
2) L'indice de réfraction du verre est $n_{1}=1.5$ et celui de l'air est $n_{2}=1.$
 
a) Quelle est la valeur maximale que peut prendre $i_{2}\ ?$
 
b) Dans ce cas, calculez la valeur correspondante de $i_{1}$ Nous l'appellerons $\lambda$
 
c) Qu'observe-t-on si $i_{1}>\lambda\ ?$
 
d) Citez au moins une application du phénomène observé en c).
 

Exercice 6

Pour la signalisation lumineuse du tableau de bord d'une machine à commande numérique, on utilise des fibres optiques (fibre représentée ci-dessous).

 

 
1) Calculer l'angle de réfraction en $A.$
 
2) Tracer le trajet du rayon lumineux dans la fibre.
 
3) Calculer l'angle d'incidence du rayon lumineux à la surface de séparation cœur-gaine.
 
4) Calculer l'angle limite à la surface de séparation cœur-gaine.
 

Exercice 7

Un rayon lumineux composé d'une lumière monochromatique rouge et d'une lumière monochromatique bleue arrive sur un prisme en verre d'angle au sommet $A=60^{\circ}$, avec un angle d'incidence $i_{1}=30^{\circ}.$
 
Les indices de réfraction du verre pour le rouge et le bleu sont respectivement $n_{R}=1.48\ $ et $\ n_{B}=1.51$
 
1) Représenter sur le schéma ci-dessous le rayon incident au point $I.$
 
2) Déterminer à un degré près les angles de réfraction $i_{2R}$ pour le rouge et $i_{2B}$ pour le bleu dans le prisme.
 
3) Tracer approximativement ces deux rayons dans le le prisme.
 
4) Quel est le rayon le plus dévié dans le prisme ?
 
5) Calculer les angles des rayons sortant du prisme $i_{3R}$ et $i_{3B}$ sachant que les angles des rayons réfractés $i_{2R}$ et $i_{2B}$ et arrivant sur la deuxième face du prisme sont donnés par les deux relations $i_{2R}'=A - i_{2R}\ $ et $\ i_{2B}'=A - i_{2B}$
 
6) Tracer les deux rayons sortant du prisme sur le schéma ci-dessous.
 
7) Quel est celui le plus dévié ?
 
8) Comment appelle-t-on ce phénomène ?
 
On donne $n_{air}=1$

 

 
 

Exercice 8

Un rayon lumineux arrive sur la surface plane , séparant l'air d'un milieu transparent , sous une incidence de $60^{\circ}.$ Sachant que l'angle de réfraction vaut $45^{\circ}.$
 
calculer l'indice relatif de réfraction de ce milieu transparent par rapport à l'air.
 
1) Calculer la valeur de l'angle de réfraction limite lorsque la lumière passe de l'air dans l'eau.
 
2) On immerge une source lumineuse de façon que la lumière se propage d'abord dans l'eau et arrive sur la surface de séparation avec un angle d'incidence $i’=60^{\circ}.$ 
 
Obtiendra-t-on un rayon réfracté dans l'air ?
 
Pourquoi ?.
 
On donne l'indice de réfraction relatif de l'eau par rapport à l'air $n=\dfrac{4}{3}$
 

Exercice 9

On schématise la réfraction d'un rayon de lumière monochromatique passant de l'air dans l'eau.

 

 
1) Reproduire et compléter ce schéma en indiquant le point d'incidence $I$, en dessinant la normale $(NN’)$ à la surface de séparation des deux milieux et en indiquant l'angle d'incidence $i_{1}$ et l'angle de réfraction  $i_{2}$( valeurs non demandées).
 
2) Donner l'expression de la seconde loi de Descartes.
 
3) Calculer l'angle de réfraction $i_{2}$ si l'angle d'incidence $i_{1}$ vaut $60^{\circ}.$
 

Exercice 10

Un rayon lumineux monochromatique arrive sur une vitre $ABCD$ faite de verre d'indice $n_{verre}=1.47$ et d'une certaine épaisseur $e.$ 
 
L'angle d'incidence sur la surface AB est $i_{1}=30^{\circ}$ (voir figure ci-dessous).

 

 
1) Calculer l'angle de réfraction $i_{2}$ du rayon dans le verre. Reproduire le schéma ci-dessus sur votre copie puis tracer ce rayon.
 
2) Déterminer l'angle d'incidence $i_{3}$ de ce rayon sur la surface $CD$ (surface de séparation entre le verre et l'air)
 
3) Avec quel angle de réfraction i$i_{4}$ le rayon émerge-t-il de la vitre ? Tracer sur votre schéma ce rayon émergent.
 
4) Comparer la direction du rayon qui arrive sur la vitre et celle de celui qui en sort. 
 
Cela dépend-il de la valeur de l'indice $n_{verre}\ ?$
 
5)Le rayon lumineux incident est de couleur blanche. 
 
Comment seront les rayons des différentes couleurs à la sortie de la vitre ? 
 
Comparer l'effet d'un prisme et l'effet d'une vitre sur la lumière blanche

 

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Équilibre d'un solide mobile autour d'un axe - 2nd S

Classe: 
Seconde
 

Exercice 1

Un chemin forestier est fermé par une barrière constituée d'une poutre (1) et d'un contre-poids (2).
 
La barrière peut tourner autour d'un axe $\Delta$ perpendiculaire en $O$ au plan de la figure

 

 
Les cotes sont en mètres. La masse de la barrière est $60\;kg\;;\ G$ est son centre de gravité.
 
Un promeneur veut la soulever en exerçant en $A$ une force $\vec{F}$ d'intensité $100\;N.$
 
1) Calculer :
 
a) l'intensité du poids $\vec{P}$ de la barrière. On donne : $g=10\;N.kg^{-1}.$
 
b) le moment de $\vec{P}$ par rapport à $\Delta.$
 
c) le moment de $\vec{F}$ par rapport à $\Delta.$
 
2) Le promeneur peut-il soulever la barrière ? Justifier la réponse
 

Exercice 2

Le chargeur représenté ci-dessous se compose:
 
$-\ $ d'un châssis et du conducteur de masse $400\;kg$ ;
 
$-\ $ de son chargement de masse $420\;kg$ ;
 
$-\ $ d'un système de levage et du godet de masse $150\;kg.$
 
Le poids du châssis s'applique au point $G_{1}$
 
Le poids du chargement au poing $G_{2}$
 
Le poids du système de levage au poing $G_{3}$

 

 
1) Calculer les intensités des poids du châssis, $P_{1}\;,\ P_{2}\ $ et $\ P_{3}$ , du chargement et du système de levage
 
2) Calculer le moment du poids $P_{1}$ par rapport à l'axe $\Delta$ de la roue avant.
 
3) Calculer le moment du poids $P_{2}$ par rapport à l'axe $\Delta$ de la roue avant.
 
4) Calculer le moment du poids $P_{3}$ par rapport à l'axe $\Delta$ de la roue avant.
 
5) Le chargeur ainsi chargé pivote-t-il autour de l'axe $\Delta\ ?$
 
6) Quelle est la charge maximale que peut transporter le godet
 
 

Exercice 3

Un solide $(S)$ de masse $m=200\;g$ est relié à un fil de masse négligeable passant par la gorge d'une poulie à axe fixe $(\Delta)$, de masse négligeable et de rayon $r.$
 
L'autre extrémité du fil est attachée à un ressort de raideur $k$ et de masse négligeable. 
 
A l'équilibre, l'axe du ressort fait un angle $\alpha=30^{\circ}$ avec l'horizontale et le ressort est allongé de $\Delta l=4\;cm.$ On néglige tout type de frottement.

 

 
1) a) Représenter les forces exercées sur le solide $(S).$
 
b) Écrire la condition d'équilibre de $(S)$ et déterminer l'expression de la tension du fil $f_{1}$, puis calculer sa valeur.
 
2) a) Représenter les forces exercées sur la poulie.
 
b) En appliquant le théorème des moments, déterminer la tension du fil $f_{2}$
 
c) Déduire la tension du fil $f_{2}$ au point $A.$
 
3) Déterminer la valeur de la raideur du ressort $k$
 
4) Par projection de la relation vectorielle, traduisant l'équilibre de la poulie, dans un repère orthonormé, montrer que la valeur de la réaction $R$ de l'axe ($\Delta$) est $R=mg\sqrt{2(1+\sin\alpha)}$
 
Calculer sa valeur.
 
On prendra : $g=10\;N.kg^{-1}$
 

Exercice 4

On dispose d'une règle homogène, de masse négligeable, pouvant tourner autour d'un axe horizontal $\Delta$ passant par son centre d'inertie $O.$ On veut connaître le comportement de la règle dans les situations suivantes
 
1) La règle, initialement au repos, est soumise à un seul couple de forces $(\vec{F}\;,\ \vec{F'})\ :$

 

 
Indiquer quel est le comportement de la règle et donner le signe du moment du couple de forces.
 
2) La règle, initialement au repos, est soumise à deux couples de forces $(\vec{F}_{1}\;,\ \vec{F}_{2})\ $ et $\ (\vec{F}_{3}\;,\ \vec{F}_{4})$ tels que

 

 
Échelle : $1\;cm\longleftrightarrow 2\;N\ $ et $\ 1\;cm\longleftrightarrow10\;cm$
 
2.1) Calculer le moment de chaque couple.
 
2.2) Exprimer la condition d'équilibre de la règle.
 
Montrer alors que la règle n'est pas en équilibre mais en rotation non uniforme. 
 
Préciser dans quel sens se fait cette rotation.
 
2.3) On veut obtenir l'équilibre de cette règle :
 
2.3.1) Pour cela, on déplace le point d'application $A_{3}$ de la force $\vec{F}_{3}$
 
Déterminer la position de $A_{3}$ par rapport à $O$ pour que la règle soit en équilibre.
 
2.3.2) Le point $A_{3}$ reprend sa position initiale : $OA_{3}=0.20\;m$ et on incline les forces $\vec{F}_{3}\ $ et $\ \vec{F}_{4}$ d'un angle $\alpha$ par rapport à la verticale comme le montre le schéma ci-dessous.

 

 
Donner l'expression du moment du couple $(\vec{F}_{3}\;,\ \vec{F}_{4})$ en fonction de $\alpha\;,\ F_{3}\;,\ A_{3}A_{4}$
 
Déterminer la valeur de $\alpha$ pour laquelle la règle est en équilibre
 

Exercice 5

Une tige rigide et homogène $(AB)$ de longueur $L$, de masse M peut tourner sans frottement autour d'un axe fixe ($\Delta$) horizontal qui lui est orthogonal passant par le point $O$ (voir figure 2).
 
Pour maintenir la tige $AB$ en équilibre suivant une direction faisant un angle $\alpha=30^{\circ}$ avec la verticale,
 
on fixe à son extrémité B un ressort à aspires non jointives , de masse négligeable et de raideur $K=10\;N.m^{-1}\;;\ OA=\dfrac{L}{4}$
 
L'axe de ressort maintenu horizontal. On donne :
 
On se propose d'étudier l'équilibre de la tige $AB.$

 

 
1) Représenter toutes les forces extérieures appliquée à la tige $AB.$
 
2) Donner l'expression de moment de chaque force par rapport à l'axe de rotation $(\Delta)$ passant par le point $O.$
 
3) Par application du théorème des moments à la tige $AB$ en équilibre , 
 
Établir l'expression de la tension du ressort exercée à l'extrémité $B$ en fonction de : $M\;,\ g\ $ et $\ \alpha$
 
4) A l'équilibre, le ressort s'allonge de $x=5\;cm.$
 
Calculer la tension du ressort.
 
En déduire la masse $M$ de la tige $AB.$ On prendra $g=10\;N.kg^{-1}$
 
5. a) Calculer la réaction de l'axe $(\delta)$ en $O.$
 
b) Déterminer l'angle $\beta$ que fait la direction de la réaction avec la verticale.
 

Exercice 6

Une barre homogène de longueur $L=AB=60\;cm$ et de masse $m=2\;kg$ peut tourner autour de son extrémité $A.$ 
 
Un fil horizontal fixé en B maintient la barre en équilibre.
 
La barre fait le plan horizontal un angle de $\alpha=15^{\circ}$

 

 
1) Représenter les forces qui s'exercent sur la barre
 
2) calculer l'intensité de la force exercée par le fil $BC$ sur la barre.
 
3) Déterminer les caractéristiques de.la réaction du sol sur la barre.
 

Exercice 7

On considère le dispositif suivant, il est formé par :

 

 
$-\ $ Une tige $AB$ de longueur $L$, de masse négligeable et mobile autour d'un axe fixe ($\delta$) placé au point $O$ (perpendiculaire au plan de la figure), tel que $OB=\dfrac{L}{4}$
 
$-\ $ Un ressort de raideur $k=30\;N.m^{-1}$, de masse négligeable et perpendiculaire à la tige au point $B$ où il est attaché.
 
$-\ $ Un solide $(S)$ de masse $400\;g$, posé sur un plan incliné de $\alpha=30^{\circ}$ par rapport à l'horizontale, et en équilibre grâce à un fil $(f)$ attaché à l'extrémité $A$ de la tige. 
 
Le plan est supposé lisse.
 
$-\ $ On prendra $g=10\;N.kg^{-1}$
 
1) a) Représenter les forces extérieures qui s'exercent sur le solide $(S)$ à l'équilibre.
 
b) Écrire la condition d'équilibre du solide $(S).$
 
c) Étudier cet équilibre et déterminer l'expression de la tension $T$ du fil $(f)$ en fonction de $m\;,\ g\ $ et $\ \alpha$
 
d) Calculer la valeur de $T$
 
2) a) Représenter les forces extérieures qui s'exercent sur la tige $AB$ à l'équilibre.
 
b) Écrire la condition d'équilibre, traduite par le théorème des moments, de la tige $AB.$
 
c) Donner l'expression du moment de chacune de ces forces.
 
d) Déduire l'expression de la tension $T_{B}$ du ressort au point $B$ en fonction de $m\;,\ g\ $ et $\ \alpha$
 
e) Calculer la valeur de $T_{B}$
 
h) Déduire l'allongement $\delta l$ du ressort.
 
3) a) Écrire la deuxième condition d'équilibre de la tige.
 
b) Étudier cet équilibre et déterminer la valeur de la réaction R de l'axe $(\delta)$ ainsi que celle de l'angle $\beta$ que fait la réaction avec la verticale
 

Exercice 8

Une tige rigide et homogène de longueur L et de masse $M=500\;g$, est suspendue par l'une de ses extrémités, notée $O$, à un axe $(\delta)$ horizontal qui lui est perpendiculaire et autour duquel elle peut tourner sans frottement .
 
On maintient la tige en équilibre suivant une direction faisant avec la verticale un angle $\alpha=30^{\circ}.$
 
L'équilibre est assuré à l'aide d'un fil de masse négligeable lié à l'extrémité libre $A$ de la tige et tendu horizontalement à l'autre extrémité du fil qui passe à travers la gorge d'une poulie on accroche un solide de masse $m$ (voir figure 1).
 
On néglige toutes les forces de frottement.

 

 
1) Quelles sont les forces extérieures appliquées à la tige ? Les représenter.
 
2)a) A l'aide du théorème des moments appliqué à la tige en équilibre, établir l'expression de la tension du fil appliquée au point $A$ en fonction de : $M\;,\ g\ $ et $\ \alpha.$
 
b) En déduire l'expression de la masse $m$ du solide. Calculer sa valeur.
 
Déterminer la valeur de la réaction de l'axe sur la tige en $O$ ainsi que l'angle $\beta$ qu'elle fait avec la verticale.
 

Exercice 9

On utilise dans cet exercice
 
$-\ $ Une sphère métallique homogène, de rayon $r=3\;cm$, de masse $M=1\;kg$
 
$-\ $ Une tige métallique de longueur $L=47\;cm$ ,très fine ,dont la masse est négligeable devant celle de la sphère. On prendra $g=10\;N.Kg^{-1}.$ 
 
On soude la tige à la sphère .Le dispositif ainsi constitué peut tourner, dans le plan vertical, autour d'un axe $(\delta)$, horizontal, passant par l'extrémité $O$ de la tige.
 
En un point $A$ de la tige, tel que : $OA=a=40\;cm$ on fixe un fil que l'on supposera toujours vertical. 
 
Lorsque le système est en équilibre la tige fait un angle $\alpha$ avec l'horizontale.

 

 
1) Représenter les forces exercées la tige à l'équilibre.
 
2) Par application du théorème des moments, établir l'expression de la tension du fil $T_{A}$ du fil appliquée en $A.$ 
 
Calculer sa valeur.
 
3) Déterminer la réaction $R$ de l'axe en $O.$
 
4) On remplace maintenant le fil par un ressort de raideur $K$ et de masse négligeable.
 
Ce ressort que l'on supposera toujours vertical n'est pas tendu lorsque la tige est horizontale. 
 
Lorsque le système est en équilibre la tige fait un angle $\Theta=6^{\circ}$ avec l'horizontale.

 

 
Calculer l'allongement du ressort à l'équilibre
 
En déduire la raideur $K$ du ressort.
 

Exercice 10

On suspend des poids différents à des distances variables afin que le système soit en équilibre et on note les résultats obtenus.
 
Expérience :
 
$m_{1}=800\;g\;;\ m_{2}=400\;g$
 
$d=1.5\;cm\;;\ D=3\;cm$

 

 
1) Faire le bilan des actions s'exerçant sur la barre à trous.
 
2) Sur la figure ci-dessus, tracer la direction de ces forces.
 
3) Déterminer les caractéristiques de ces forces lorsque cela est possible.
 
4) Calculer le moment de chaque force
 
5) Calculer la somme des moments des forces s'exerçant sur la une barre à trous
 

Exercice 11

On donne $g=10\;N.Kg^{-1}$
 
Une tige $AB$ de masse $m$, de longueur $L=60\;cm$, homogène, de section constante, mobile autour d'un axe horizontal ($\delta$) orthogonal à la tige passant par son extrémité $A.$ 
 
A son extrémité $B$ on exerce une force $F_{B}$ de même direction que la tige et de valeur $4\;N.$ 
 
Au point $C$ tel que $AC=\dfrac{L}{4}$ est appliquée une force $F_{C}$ de direction verticale dirigée vers le haut et de valeur $6\;N$ (Voir figure)

 

 
1.1) Faire le bilan des forces extérieures exercées sur la tige.
 
1.2) Calculer la valeur algébrique des moments par rapport à l'axe $\delta$ des forces $F_{B}\ $ et $\ F_{C}.$
 
2) Sachant que la tige est en équilibre dans cette position.
 
2.1) Calculer la valeur algébrique du moment du poids par rapport à l'axe $\delta.$
 
2.2) Déduire la masse $m$ de la tige.
 
3) La direction de la force $F_{B}$ fait maintenant un angle $\alpha=30^{\circ}$ avec celle de la tige (Voir figure 2).

 

 
Que deviennent le sens et la valeur de la force $F_{C}$ pour que la tige garde la même position d'équilibre.
 

Exercice 12

Le schéma ci-dessous représente un cabestan (treuil) : il est constitué de deux manivelles solidaires d'un tambour $(t)$ d'axe $O$, sur lequel s'enroule un câble tendu.
 
Les mains exercent, aux extrémités des manivelles, deux forces $F_{1}\ $ et $\ F_{2}$ parallèles et de même intensité $100\;N$
 
Le câble exerce, en $A$, sur le tambour, une force $\vec{F}_{c/t}$  verticale. 
 
l'ensemble des autres forces d'exerçant sur le treuil est équivalent à une force $R$ exercée en $O.$

 

 
1) Quel est le moment de la force $\vec{R}$ par rapport à $O\ ?$
 
2) Calculer le moment du couple $(\vec{F_{1}}\;,\ F_{2})$
 
3) Sachant que le treuil est en équilibre dans cette position, en déduire l'intensité de la force exercée par le câble tendu sur le tambour (on donne $OA=6.5\;cm)$
 

Exercice 13

I Un mobile est constitué de 3 poulies solidaires entre elles pouvant tourner autour du même axe. 
 
On attache un fil à chaque poulie et une masse.

 

$$M_{1}=200\;g\quad R_{1}=5\;cm$$
$$M_{2}=300\;g\quad R_{2}=10\;cm$$
$$M_{3}=100\;g\quad R_{3}=16\;cm$$
1) Le solide est il en équilibre ? 
 
$\ast\ $ S'il ne l'est pas, dans quel sens tourne t-il ? 1 ou 2 ? Pourquoi ?
 
2) Par quelle masse devrait-on remplacer $M_{2}$ pour qu'il soit en équilibre ?
 
3) Si $M_{2}$ était toujours égale à $300\;g$, à quelle distance de l'axe $R_{3}$ devrait-on attacher $M_{3}$
 

Exercice 14

1) Le pont-levis est mobile autour de l'axe horizontal $O.$ Il est constitué d'un plateau de poids $P=5000\;N$ et dont le centre d'inertie $G$ est au milieu de $OA.$ 
 
Il est maintenu en équilibre, dans la position correspondant à $\alpha=60^{\circ}$, grâce au contre poids $C$ et à la corde $ABC$ dont on néglige la masse. $OA=OB=4\;m.$
 
Calculer la tension $T$ de la corde dans ces conditions, puis sa tension $T'$ lorsque le pont est abaissé mais sans reposé.
 
2) Soit un treuil de masse $M=20\;kg$ ; il permet de soulever une charge de $1200\;N.$ 
 
Déterminer le module de la force $F$ qu'il faut exercer perpendiculairement à $OA$ pour soulever la charge

 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 

 

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Équilibre d'un solide soumis à des forces - 2nd S

Classe: 
Seconde
 

Exercice 1 : Équilibre d'un solide relié à un fil sur un plan incliné.

1) Un solide $S$ de poids $P=100\;N$ est maintenu en équilibre sur un plan incliné d'un angle $\alpha$ par rapport à l'horizontal grâce à un fil (figure.1 ci-dessous).

 

 
Le support du plan incliné $AB$ est lisse.
 
1.1) Faire le bilan des forces appliquées au solide $(S).$
 
1.2) Représenter ces forces puis déterminer leurs intensités par la méthode analytique.
 
2) Un solide $(S')$ de poids $P'$ glisse sur un support oblique $A'B'$ (figure.2 ci-dessus) . 
 
La partie $A'C$ de ce plan est rugueuse et la partie $CB'$ lisse.
 
a) Le solide $S'$ s'arrête entre $A'\ $ et $\ C.$
 
Exprimer les composantes tangentielle $f$ et normale $R_{n}$ de la réaction du plan $A'C$ en fonction de $P'\ $ et $\ \alpha$
 
Comparer la direction de cette force de réaction à celle du vecteur poids du solide $S'.$
 
b) On déplace le solide $S'$ et on le pose sur le plan $CB'$ au-delà du point $C$ (figure.2). 
 
Il glisse puis se met en contact avec un ressort de constante de raideur $k.$ 
 
Le solide $S'$ s'immobilise alors quand le ressort est comprimé d'une quantité $x.$ 
 
Représenter les forces s'exerçant sur le solide $S'$ dans cet état d'équilibre puis exprimer l'intensité de la force exercée par le ressort sur $S'$ en fonction de $P'\ $ et $\ \alpha.$
 
c) Considérant les résultats a) et b), exprimer l'intensité $f$ des forces de frottement du plan $A'C$ en fonction de $x$ et de $k.$
 
d) Calculer dans l'ordre $f\;,\ R_{n}$, la réaction $R$ du plan $A'C$, et la masse $m'$ du solide $S'.$
 
On donne : $k=50\;N.m^{-1}\;;\ g=10\;N.kg^{-1}\;;\ x=8\;cm\;;\ \alpha=30^{\circ}$
 
e) Calculer l'angle $\beta$ que fait la direction de la réaction du plan, $A'C$ avec celle du plan incliné $A'B'.$
 

Exercice 2

Un véhicule de masse $820\;kg$ est immobilisé sur un plan incliné à l'aide d'un câble fixé au point $A.$
 
Les frottements sur le sol sont négligés. Le plan est incliné de $30^{\circ}$ par rapport au plan horizontal.
 
1) Faire le bilan des forces s'exerçant sur le véhicule;
 
2) Déterminer par méthode graphique les intensités des forces inconnues.
 
On prendra $g =10\;N.kg^{-1}$. Échelle : $1\;cm$ pour $2000\;N$
 
3) Retrouver ces intensités par méthode analytique
 
N.B : la réaction exercée par le sol sur le véhicule par l'intermédiaire des 4 roues est assimilée à une force unique appliquée en $G$ et de direction perpendiculaire au plan incliné

 

 

Exercice 3

On dispose de 2 ressorts . Le ressort $(R_{1})$ a une longueur à vide $l_{01}$ de $10\;cm$ et s'allonge de $1\;cm$ pour une force appliquée de $1\;N.$
 
Le ressort $(R_{2})$ a une longueur à vide $l_{02}=15\;cm$ et s'allonge de $4\;cm$ pour une force appliquée de $1\;N.$
 
On les réunit à un anneau de poids et de dimensions négligeables. 
 
Les 2 autres extrémités des ressorts sont fixées à 2 crochets distants de $30\;cm.$ 
 
Soient $l_{1}\ $ et $\ l_{2}$ les longueurs respectives des ressorts $(R_{1})\ $ et $\ (R_{2}).$
 
Calculer de la longueur de chaque ressort $l_{1}\ $ et $\ l_{2}$ et les forces de tension $F_{1}\ $ et $\ F_{2}$ des ressorts

 

 

Exercice 4

On veut déterminer par le calcul la masse $m$ et l'angle $\alpha$, dans la situation décrite ci-dessous.
 
On a : $m_{1}=150\;g\;;\ m_{2}=100\;g\ $ et $\ \beta=90^{\circ}.$

 

 
1) Représenter sur un schéma les forces qui s'exercent sur l'anneau
 
2) Rappeler la relation vectorielle que l'on peut écrire à l'équilibre.
 
3) Le plan est muni d'une base orthonormé ${O\;,\ \vec{i}\;,\ \vec{j}}.$ 
 
Donner l'expression de toutes les forces agissant sur l'anneau en fonction des vecteurs $\vec{i}\ $ et $\ \vec{j}$ de la base et de l'intensité de chacune des forces.
 
4) En déduire 2 équations permettant de calculer $\alpha\ $ et $\ m.$
 
5) Calculer $\tan\alpha$ pour en déduire la valeur de $\alpha$ puis de $m.$
 
6) Vérifier vos valeurs trouvées à celle qui sont mesurables expérimentalement.
 

Exercice 5

I) Un ressort à spires non jointives de longueur $L_{0}$ et de masse négligeable.
 
Dans le but de déterminer la raideur $K$ de ressort, on mesure sa longueur $L$ pour des valeurs différentes de la tension de ressort $T$ ; On donne la courbe suivante :

 

 
1) Donner l'expression de $T$ en fonction de $K\;,\ L\ $ et $\ L_{0}$
 
2) Déduire a partir du graphique : $T(N)$
 
a) La raideur $K$ du ressort en $N.m^{-1}$
 
b) La longueur $L_{0}$ du ressort en $cm$
 
II) Le ressort précédent est disposé de la manière suivante :
 
A l'équilibre de solide la longueur du ressort est $l=18\;cm$ .
 
1) Représenter les forces exercées sur le solide a l'équilibre.
 
2) Calculer la tension du ressort.
 
3) En déduire la masse m du solide $(S).$ On donne $g=9.8\;N.kg^{-1}$

 

 
 

Exercice 6

Un corps $(C)$ de poids $P=20\;N$ repose sans frottement sur un plan incliné faisant un angle $\alpha=30^{\circ}$ par rapport à l'horizontale. 
 
Il est maintenu fixe à l'aide d'un ressort de masse négligeable, de raideur $k=500\;N.m^{-1}$, de longueur initiale $L_{0}=20\;cm$ et faisant un angle $\beta=15^{\circ}$ par rapport au plan incliné.

 

 
1) Représenter les forces exercées sur le corps $(C).$
 
2) Écrire la condition d'équilibre du corps $(C).$
 
3) Déterminer la valeur de la tension $T$ du ressort.
 
4) Déduire sa longueur $L.$
 
5) En réalité les frottements ne sont pas négligeables et sont équivalentes à une force $f$ parallèle au plan incliné et dirigée vers le haut. 
 
La valeur de la tension du ressort est dans ce cas $T'=8.4\;N$
 
Écrire la nouvelle condition d'équilibre du corps $(C)$ et déduire la valeur de la force de frottement $f$
 

Exercice 7

I) Soit un ressort à spires non jointives, de longueur initiale $L_{0}$ et de masse négligeable
 
Afin de déterminer sa raideur K on accroche un solide $(S_{1})$ de masse $m_{1}=100\;g$, la longueur de ressort est $L_{1}=20\;cm.$ 
 
On remplace $(S_{1})$ par un solide $(S_{2})$ de masse $m_{2}=175\;g$ la longueur de ressort devient $L_{2}=23\;cm$

 

 
1-a) Établir l'expression de K en fonction de $m_{1}\;;\ m_{2}\;;\ g\;;\ L_{1}\ $ et $\ L_{2}$ 
 
Montrer que $K=\dfrac{(m_{2}-m_{1})}{l_{2}-l_{1}}g$
 
Calculer sa valeur en $N.m^{-1}$
 
b) En déduire la longueur initiale $L_{0}$ du ressort.
 
II) Avec le ressort précédent, on réalise le système schématisé ci-dessous ; le solide $(S')$ de masse $m'$ est accroché d'une part au ressort, d'autre part à un fil (voir figure).
 
A l'équilibre, la direction de fil fait un angle $\alpha=60^{\circ}$ avec la verticale d'une part et d'autre part elle est perpendiculaire à celle de l'axe du ressort. Soit $L=18\;cm$ ; la longueur de ressort à l'équilibre.
 
1) Représenter toutes les forces exercées sur $(S')$
 
2) Établir en fonction de $m'\;,\ g\ $ et $\ \alpha$
 
2.1) La tension de ressort $T_{1}$
 
2.2) La tension du fil $T_{2}$
 
2.3) Calculer leurs valeurs
 
3) En déduire la masse $m'$ de solide $(S')$
 

Exercice 8

Une tige rigide est maintenue incliné d'un angle $\alpha=60^{\circ}$ par rapport à la verticale. 
 
Un ressort à spires non jointives, de masse négligeable de longueur à vide $L_{0}=12\;cm$, de raideur $k=50N.m^{-1}$ est enfilé le long de la tige. 
 
L'une des extrémités de la tige est fixé en un point $I$ de la tige, l'autre extrémité est attachée à un solide de masse $m=80\;g$ (voir figure)
 
1) Représenter toutes les forces appliquées au solide.
 
2.a) Exprimer la tension du ressort en fonction de $m\;,\ g\ $ et $\ \alpha.$ 
 
Calculer sa valeur. On prendra $g=9.8N.kg^{-1}$
 
On donne : $\sin\alpha=0.86\ $ et $\ \cos\alpha=0.5$
 
b) En déduire la valeur de l'allongement du ressort a l'équilibre.
 
3) Exprimer la réaction $R$ de la tige en fonction de $m\;,\ g\ $ et $\ \alpha.$ Calculer sa valeur

 

 
 

Exercice 9

1) un ressort à spires non jointives de longueur $L_{0}=20\;cm$ de masse négligeable et de raideur $k=25\;N.m^{-1}.$
 
Ce ressort disposé verticalement est fixé par son extrémité supérieure, à son extrémité inférieure, on suspend un solide de masse $m=100\;g.$ 
 
Déterminer la longueur $L$ du ressort à l'équilibre de solide.
 
2) le ressort et le solide précédent sont placés comme l'indique la figure.
 
on suppose que le solide repose sans frottement appréciable sur le plan incliné d'un angle $\alpha$ par rapport à la direction verticale.
 
L'axe de ressort est parallèle à la ligne de plus grande pente de plan incliné.

 

 
a) représenter toutes les forces extérieures agissant sur le solide.
 
b) calculer la tension de ressort sachant que la longueur de ressort a l'équilibre est $L=18\;cm.$
 
c) Établir les expressions de la tension de ressort ainsi que la réaction $R$ de plan en fonction de : $m\;,\ g\ $ et $\ \alpha.$ Calculer $\alpha\ $ et $\ R.$
 
On donne :
 
$g=10Nkg^{-1}\;;\ \cos60=0.5\;;\ \sin60=0.86\;;\ \cos30=0.86\;;\ \sin30=0.5$
 
3) On ajoute au solide précédent un solide $(S')$ de masse $(m').$ 
 
La longueur du ressort devient $L’=16.5\;cm$. Déterminer $m'.$
 

Exercice 10

Une charge de masse $m=50\;kg$ est suspendue au plafond à l'aide de 2 fils.

 

 
1) Faire le bilan des forces qui s'appliquent à la charge
 
2) Déterminer la tension dans chaque fil pour $\alpha=30^{\circ}\ $ et $\ \alpha=70^{\circ}.$
 

Exercice 11

Une petite bille d'acier, de poids $P=5.10^{-2}\;N$, est attachée à un support vertical par un fil de nylon $AO$
 
En outre, un aimant exerce sur elle une force magnétique horizontale attractive.
 
A l'équilibre, le fil est incliné d'un angle $\alpha=20^{\circ}.$
 
Calculer l'intensité de la force magnétique ainsi que la valeur de la tension du fil.

 

 
 

Exercice 12

Une charge de poids $P=100\;N$ est soutenue par 2 fils $AB\ $ et $\ BC$ qui font respectivement, avec la verticale, des angles de $60^{\circ}\ $ et $\ 30^{\circ}.$
 
Calculer les tensions des 2 fils à l'équilibre

 
 

 
 

Exercice 13

Deux objets sont suspendus par l'intermédiaire de deux fils 1 et 2.
 
On donne : masse de $(S_{1})=1\;kg$ et masse de $(S_{2})=2\;kg$ ; la masse des fils est négligeable.

 

 
1) Déterminer à l'équilibre la tension du fil 2.
 
2) Déterminer à l'équilibre la tension du fil 1
 

Exercice 14

Un cube homogène, d'arête a égale à $10\;cm$, est fabriqué dans un matériau de masse volumique $\rho_{c}$, immergé dans l'eau et suspendu à un ressort vertical en $B$, le centre d'une face ; il est en équilibre.

 

 
1) Déterminer les valeurs du poids $P$ du cube et de la poussée d'Archimède $F$ exercée par l'eau sur le solide.
 
2) Le solide étant en équilibre, les forces extérieures appliquées à ce cube sont colinéaires et leur direction passe par $G$ centre d'inertie du cube. 
 
Déterminer la valeur de la force de rappel $T$ du ressort.
 
3) Déterminer l'allongement du ressort. 
 
Données : $g=10\;N.kg^{-1}\;;\ \rho_{c}=9.10^{3}kg.m^{-3}\;;\ k=100\;N.m^{-1}$
 

Exercice 15

Un solide $(S)$, homogène de masse $100\;kg$ est maintenu en équilibre sur un plan incliné rugueux d'un angle $\alpha=30^{\circ}.$ par rapport au plan horizontal,
 
Le solide est plus relié à un câble par un fil AB faisant un angle, $\beta=25^{\circ}$ avec la ligne de grande pente.
 
Les forces de frottements sont modélisées par le vecteur $\vec{f}$, parallèle à la ligne et d'intensité $f=20\;N.$
 
1) Faire le bilan des forces s'exerçant sur le solide $(S)$
 
2) Représenter qualitativement ces forces sur la figure
 
3) Déterminer l'intensité de la tension du fil $AB$
 
4) Calculer la réaction du plan incliné et donner sa direction

 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 

 

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Le poids - La masse - Relation entre poids et masse - 2nd S

Classe: 
Seconde
 

Exercice 1

Un solide en aluminium de masse $m=30\;g$ et de volume $V=12\;cm^{3}.$
 
1) Calculer sa masse volumique $\rho$ en $g.cm^{-3}$ puis en $kg.m^{-3}$.
 
2) Calculer sa densité d par rapport à l'eau (on donne : $\rho_{eau}=1\;g.cm^{-3}$)
 
3) Sachant que la masse volumique de l'aluminium est $\rho_{Al}=2.7\;g.cm^{-3}$ écris "Vrai" ou "faux" devant chacune des affirmations suivantes :
 
a) Si le solide est plein alors il est en aluminium pur.
 
b) Si le solide est plein alors il est un alliage d'aluminium et d'un autre métal de masse volumique inférieure à $2.7\;g.cm^{-3}.$
 
c) Si le solide est en aluminium pur alors il est plein.
 
4) Sachant que le solide est en aluminium pur.
 
a) Montre que 'il est creux.
 
b) Détermine le volume $V_{c}$ de la cavité située à l'intérieure du solide
 

Exercice 2

Un corps solide $(S)$ de masse $m=75\;g$ a la forme d'un cube d'arête $a=5\;cm.$

 

 
1) Calculer le volume du solide $(S).$
 
2) Calculer la masse volumique du solide $(S)$ en $g.cm^{-3}$ et en $kg.m^{-3}.$
 
3) Quelle est la nature du solide $(S)$ en utilisant le tableau ci-dessous
$$\begin{array}{|c|c|c|c|c|}\hline\text{Corps}&\text{Aluminium}&\text{Cuivre}&\text{Liège}&\text{Bois}\\\hline\rho\,(kg.m^{-3})&2700&8900&240&600\\\hline\end{array}$$
4) Calculer la densité du solide $(S)$ par rapport a l'eau.
 
On donne : la masse volumique de l'eau $\rho_{eau}=1000\;kg.m^{-3}.$
 
5) On introduit le solide $(S)$ dans un récipient contenant de l'eau. Dire en justifiant la réponse si le solide $(S)$ coule ou flotte "se situer au font du récipient ou a la surface de l'eau".
 

Exercice 3

I. Un commerçant désire acheter de l'huile pure, il pratique la démarche expérimentale suivante en utilisant un échantillon d'huile comme le montre la figure suivante :

 

 
1) A partir des pesées précédentes, calculer :
 
a) La masse $m$ d'eau
 
b) La masse $m'$ d'huile
 
c) On donne $\rho_{eau}=1\;g.cm^{-3}$
 
Déduire le volume d'eau $V$ contenu dans le flacon en $cm^{3}$ puis en $l.$
 
2) a) Déterminer la densité $d'$ de l'huile par rapport à l'eau.
 
b) Sachant que la masse volumique  $\rho_{huile}=0.92\;g.cm^{-3}$ Conclure
 
II. On dispose d'un bêcher de capacité $100\;ml$ et d'un corps $C$ de forme cubique de $4\;cm$ de côté
 
1) Calculer le volume $V$ du corps $C.$
 
2) a) Peut-on mesurer le volume du corps $C$ en l'introduisant dans un bêcher contenant $50\;ml$ d'eau ?
 
Pourquoi ?
 
3) Calculer le volume d'eau déversée $V_{D}$ lorsqu'on met le corps $C$ dans le bêcher
 

Exercice 4

Soient deux liquides $L_{1}\ $ et $\ L_{2}.$ On réalise les expériences schématisées ci-dessous.
 
1.a) Déterminer la masse $m_{1}$ du liquide $L_{1}.$

 

 
b) Calculer la masse volumique $\rho_{1}$ du liquide $L_{1}$ en $g.cm^{-3}$ puis en $kg.m^{-3}$
 
c) Déduire la densité $d_{1}$ du liquide $L_{1}$ par rapport à l'eau.
 
2.a) Déterminer la masse $m_{2}$ du liquide $L_{2}.$
 
b) Calculer la masse volumique $\rho_{2}$ du liquide $L_{2}$ en $g.cm^{-3}$ puis en $kg.m^{-3}$
 
c) Déduire la densité $d_{2}$ du liquide $L_{2}$ par rapport à l'eau.
 
3) Lequel de ces deux liquides est le plus dense ? Justifier la réponse.
 
4) On mélange ces deux liquides.
 
a) Quel est la nature du mélange obtenu.
 
b) Calculer la masse volumique du mélange.
 

Exercice 5

Le poids d'un corps est une grandeur physique exprimée en Newton $(N)$ qui indique la force de pesanteur d'origine gravitationnelle exercée par la Terre sur un corps massique.
 
Le poids se mesure avec un dynamomètre, instrument de mesure muni d'un ressort dont l'allongement correspond au poids du corps qui y est suspendu. On réalise les mesures suivantes :

 

 
1) Compléter le tableau de mesures suivants :
$$\begin{array}{|c|c|c|c|c|c|c|}\hline\text{Masse }m\text{ (en }g)&0&100&200&400&700&1000\\\hline\text{Poids }P\text{ (en }N)&&&&&&\\\hline\end{array}$$
 
2) Sur le papier millimétré, construire la courbe donnant le poids $P$ en fonction de la masse $m.$
 
3) Quelle est l'allure de la courbe obtenue ?
 
4) Que peut-on en déduire pour le poids et la masse ?
 

Exercice 6 : Réalisation d'un dynamomètre

Donnée : on prendra $g=10\;N.kg^{-1}$

 

 
Pour réaliser un dynamomètre à l'aide d'un ressort, on effectue un étalonnage. 
 
Pour cela, le ressort est suspendu à un point fixe par une de ses extrémités. 
 
L'autre extrémité porte un index et se déplace devant une règle maintenue verticalement par un support fixe.
 
On accroche à l'extrémité libre différente masses marquées et on lit, à l'équilibre, les indications correspondantes de l'index sur la règle graduée.
 
On obtient :
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline m\;(kg)&0&0.20&0.40&0.60&0.80&1&1.20&1.40&1.60&1.80&2\\ \hline x\;(cm)&0&2.6&5.2&8&10.7&13.3&16&18.6&21.5&24&26.5\\ \hline\end{array}$$
1) On considère le système "masse marquée" dans le référentiel terrestre.
 
a) Quelles sont les forces qui agissent sur le système à l'équilibre ? 
 
(Donner toutes les caractéristiques sans calculer aucune norme).
 
b) Que peut-on dire de la somme de ces forces et pourquoi ?
 
c) En déduire une relation entre $m$ (valeur de la masse suspendue) et $T$ (norme de la force exercée par le ressort sur la masse).
 
2) Construire le graphique donnant $T$ en fonction de $x.$ Que représente cette longueur ?
 
3) En déduire, en justifiant, la valeur de la raideur du ressort et son unité.
 
Applications :
 
4.a) On souhaite se servir du dispositif réalisé pour déterminer le volume d'une boite. 
 
On suspend la boite à l'extrémité libre du ressort : l'index indique alors: $x_{1}=16\;cm.$
 
En déduire sa masse en utilisant le graphique.
 
b) On immerge maintenant complètement la boite dans une bassine remplie d'eau de façon à ce que la boite ne touche aucune paroi.
 
L'index indique alors $x_{2}=10\;cm$
 
$-\ $ Pourquoi la valeur indiquée par l'index a-t-elle diminuée ?
 
$-\ $ Faire un schéma des forces appliquées sur le système.
 
$-\ $ En déduire l'expression littérale du volume de la boite. Calculer sa valeur.
 
5) On utilise maintenant le ressort pour tester la résistance d'une colle. 
 
Pour cela, on colle un petit disque en plastique sur un support et on laisse bien sécher. 
 
On fixe ensuite une extrémité du ressort au centre du disque. On tend lentement le ressort, perpendiculairement au disque, jusqu'à l'arrachement
 
Juste avant que le disque ne se décolle, le ressort était étiré de $20\;cm.$
 
Déterminer graphiquement la valeur de la force nécessaire pour produire l'arrachement
 

Exercice 7

Pour déterminer la densité du fer, on réalise les deux expériences suivantes :

 

 
1) Déterminer la masse $m$ du fer.
 
2) Déterminer le volume $V$ du fer
 
3) En déduire la masse volumique $\rho_{Fer}$ du fer dans SI.
 
4) Calculer la densité $d$ du fer. Sachant que $\rho_{eau}=1\;g.cm^{-3}$
 
5) Expliquer Pourquoi si on lance un clou de fer dans l'eau il tombe au fond
 

Exercice 8

Un solide plein en fer de forme cubique et d'arête $a=2\;cm$ a une masse $m_{fer}=63.2\;g$
1) Déterminer, en $cm^{3}$, le volume $V$ du solide.
 
2) Proposer une autre méthode permettant de déterminer ce volume. Faire un schéma.
 
3) a) Rappeler l'expression de la masse volumique en précisant la signification de chaque terme.
 
b) Montrer que la masse volumique du fer est $\rho_{fer}=7,9 g.cm^{-3}$.
 
4) On réalise les équilibres suivants :

 

 
4) a) Déterminer, en $g$, la masse $m$ eau du volume $V=8\;cm^{3}$ d'eau.
 
4) b) Exprimer la densité d du fer par rapport à l'eau en fonction de $m_{fer}$ et $m_{eau}.$
 
4) c) Calculer $d.$
 
4) d) Le fer flotte-t-il sur l'eau ? Justifier la réponse.
 

Exercice 9

Un cylindre plein en plomb à une hauteur de $10\;cm$ et de rayon de $2\;cm$
 
La pesée de ce cylindre est représentée par la figure

 

 
On donne : $m=1,5\;kg\;,\ m_{1}=80\;g$ ; la masse volumique de l'eau $\rho_{e}=1000\;kg.m^{-3}$
 
1.a) Calculer le volume de cylindre
 
b) Déterminer sa masse
 
2.a) Déduire la masse volumique du plomb en $g.cm^{-3}$ puis en $kg.m^{-3}$
 
b) Déterminer la densité du plomb par rapport à l'eau
 
c) Si on introduit ce cylindre dans une éprouvette non graduée contient de l'eau quelle sera alors la hauteur de l'eau dans l'éprouvette ?
 
3) Un morceau de fer de forme sphérique de masse $m=7.9\;g$ déterminer le volume de ce sphère sachant que la densité du fer $d_{fer}=7900.$
 

Exercice 10

On réalise les équilibres suivants en utilisant la même tare, le liquide utiliser et l'huile

 

 
1) Écrire les égalités correspondantes pour chaque équilibre
 
2) Déduire la masse de l'huile
 
3) Déterminer la masse volumique de l'huile en $g.cm^{-3}\ $ et $\ kg.m^{-3}$
 
4) Déterminer la densité de l'huile par rapport à l'eau. Conclure 
 
On donne $\rho_{e}=1\;g.cm^{-3}$
 
5) Si on refait les mêmes expériences on remplace l'huile par $10\;cm^{3}$ de mercure on trouve $m_{1}=230\;g\ $ et $\ m_{2}=94\;g$
 
a) Déterminer la masse de mercure
 
b) Déterminer la masse volumique du mercure en $g.cm^{-3}\ $ et $\ kg.m^{-3}$
 
c) Déterminer la densité du mercure par rapport à l'eau. Conclure
 
6) On mélange dans un récipient de l'eau, de l'huile et du mercure représenter sur un schéma le mélange hétérogène obtenu expliquer
 

Exercice 11

Un pavé flotte à la surface de l'eau. Ses dimensions sont : hauteur : $20\;cm$ ; longueur : $60\;cm$ ; largeur : $20\;cm$

 

 
1) Le pavé émerge sur une hauteur de $3\;cm.$ Calculer le volume de la partie immergée.
 
2) Calculer la masse d'eau déplacée. $\rho_{eau}=1000\;kg.m^{-3}$
 
3) Calculer le poids d'eau déplacé et en déduire la valeur du poids du pavé. $g=10\;N.kg^{-1}$
 
4) Calculer la masse du pavé.
 
5) a) Calculer le volume du pavé.
 
b) Préciser le matériau constituant ce pavé :
$$\begin{array}{|l|c|c|c|c|c|}\hline\text{Matériau}&\text{Polystyrène}&\text{Bois}&\text{Glace}&\text{Aluminium}&\text{Fer}\\\hline\text{Masse volumique }kg.m^{-3}&11&850&920&2700&8000\\\hline\end{array}$$
 

Exercice 12

Un iceberg a un volume total $V_{T}= 600\;m^{3}$
 
Sa masse volumique (glace) est $\rho_{1}=910\;kg.m^{-3}$, celle de l'eau de mer est $\rho_{2}=1024\;kg.m^{-3}$
 
1) Schématiser l'iceberg flottant et préciser les forces auxquelles il est soumis lorsqu'il est à l'équilibre.
 
2) Calculer la masse totale de l'iceberg.
 
3) Calculer le volume immergé (sous l'eau) $V_{i}$ de l'iceberg
 
4) Trouver une relation entre le Volume immergé $V_{i}$ , le volume total $V_{T}$ et les masses volumiques.
 
5) En déduire la proportion (pourcentage) de glace immergée dans cet iceberg.
 

Exercice 13 : Sur la Lune

Lors d'une mission lunaire, un astronaute a mesuré les poids $P$ de différents objets de masses $m$ connues.
 
Il obtient les résultats suivants :
$$\begin{array}{|c|c|c|c|c|c|}\hline m\;(kg)&0.30&0.50&0.80&1.10&1.50\\ \hline P\;(N)&0.49&0.82&1.30&1.79&2.45\\ \hline\end{array}$$
 
1) Tracer la courbe traduisant la variation de P en fonction de $m.$ Tu prendras :
 
$-\ $ en abscisse, $0.5\;cm$ pour $0.10\;kg$
 
$-\ $ en ordonnées, $0.5\;cm$ pour $0.20\;N$
 
2) En Déduire la valeur de l'intensité de la pesanteur lunaire $g$ (On expliquera la démarche)
 
3) L'expression de l'intensité de la pesanteur à la surface de la Lune est donnée, en première approximation, par la relation :
 
$g=6.67.10^{-11}\dfrac{M}{R^{2}}$  où $M\ $ et $\ R$ sont respectivement la masse en kilogramme de la Lune et son rayon en mètre.
 
$R=1738000\;m$
 
En déduire la masse de la Lune
 

Exercice 14

François soupçonne que les petits soldats avec lesquels il joue ne sont pas en plomb.
 
Il dispose d'échantillons de plusieurs métaux gris (argent, zinc, fer et plomb), d'une éprouvette graduée et d'une balance électronique. 
 
François fait ses mesures et remplit le tableau suivant. N'ayant pas vidé son éprouvette il la renverse sur sa feuille de résultats et se retrouve avec une feuille à trous
$$\begin{array}{|l|c|c|c|c|c|}\hline\text{Métal}&\text{Fer}&\text{Plomb}&\text{Zinc}&\text{Argent}&\text{Soldat}\\ \hline\text{Masse de l'échantillon }(g)&45&&29.7&76.9&81.4\\ \hline\text{volume de l'échantillon }(ml)&&6.5&11&&7.2\\ \hline\text{Masse volumique }(g.ml^{-1})&7.8&11.3& &10.5& \\ \hline\end{array}$$
1) Expliquer en quelques phrases comment il doit s'y prendre pour vérifier la composition de ses soldats.
 
2) A quoi va servir l'éprouvette graduée ? Comment va-t-il s'en servir ?
 
3) Recopier et compléter le tableau en faisant apparaître tous les calculs.
 
4) Conclure quant au soupçon de François. Justifier
 
Exercice 15 : Équilibre d'un iceberg
 
Rappel : Théorème d'Archimède : "tout corps immergé dans un fluide subit de la part de celui-ci, une poussée verticale, de bas vers le haut, égale au poids du fluide déplacé"
 
On considère un iceberg de volume total $V$ et de volume émergé $V'.$
 
1) Schématiser l'iceberg dans son état d'équilibre (les 3/4 de sa hauteur sont immergés).
 
2) Faire le bilan des forces appliquées à l'iceberg. Représenter ces forces sans considération d'échelle.
 
3) Énoncer la condition d'équilibre de l'iceberg. En déduire l'expression de $V$ en fonction de $\rho_{e}$ (masse volumique de l'eau), $\rho_{i}$ (masse volumique de l'iceberg) et $V’.$
 
4) Calculer alors dans l'ordre $V$ et la masse $M$ de l'iceberg.
 
Données : $\rho_{i}=910\;kg.m^{-3}\;;\ \rho_{e}=1024\;kg.m^{-3}\;;\ V'=600\;m^{3}$

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 

 

 
Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Généralités sur les forces - 2nd S

Classe: 
Seconde
 

Exercice 1 Mots croisés sur les forces



 
Horizontalement
 
4) Longueur d'un vecteur
 
5) Outil mathématique permettant la représentation d'une force
 
10) Elles s'exercent par contact
 
13) Grandeur d'une force
 
15) Se dit du point où s'exerce une force
 
16) Effet d'une action mécanique pouvant causer la déformation d'un objet
 
17) Effet d'une action mécanique pouvant provoquer,empêcher ou modifier le mouvement
 
18) Forces qui s'exercent mutuellement sur les deux objets
 
Verticalement
 
1) Outil permettant la mesure de l'intensité d'une force
 
2) Elle s'applique un point précis
 
3) Actions mécaniques qui s'exercent sans qu'un contact
 
6) Action mécanique qui s'exerce sur une surface
 
7) Changer la nature du mouvement d'un corps est un ... d'une force
 
8) Du haut vers le bas par exemple
 
9) Action capable de provoquer ou de modifier un mouvement, de maintenir en équilibre ou de déformer un corps
 
11) Action mécanique qui déformer un corps
 
12) Unité de force et anglais célèbre
 
14) La verticale en est une, l'horizontale aussi
 

Exercice 2

1) Lire les résultats donnés par les dynamomètres dans les cas suivant.

 

 
2) Une force dont l'intensité est égale à $125\;N$ est représentée par un vecteur qui mesure $5\;cm$.
 
Quelles seraient les mesures des longueurs des vecteurs qui représenteraient des forces de $25\;N\;,\ 300\;N\;,\ 480\ ?$
 
3) On a représenté des forces par des vecteurs. 
 
Classer celles qui ont une ou plusieurs caractéristiques communes : direction, sens,....

 

 
 

Exercice 3

1) Anna est sur une luge tirée par Arthur avec une force $\vec{F}_{1}$ et poussée par Alain avec une force $\vec{F}_{2}$
Sachant que l'échelle utilisée est de 1 cm pour 50 N, caractériser $\vec{F}_{1}\ $ et $\ \vec{F}_{2}.$

 

 
$$\begin{array}{|c|c|c|c|c|}\hline\text{Force}&\text{Point}&\text{Direction}&\text{Sens}&\text{Valeur (N)}\\&\text{d'application}&&&\\\hline\vec{F}_{1}&&&&\\ \hline\vec{F}_{2}&&&&\\ \hline\end{array}$$
2. Le symbole ci-dessus a été utilisé à Mexico, lors des jeux olympiques de 1968.
 
On s'intéresse à la force $\vec{F}$ exercée par l'athlète sur l'anneau.
 
2.1. Donner la nature de l'action.
 
2.2. Caractériser et représenter la force $\vec{F}$ de valeur $450\;N$.
$$\begin{array}{|c|c|c|c|c|}\hline\text{Force}&\text{Point}&\text{Direction}&\text{Sens}&\text{Valeur (N)}\\&\text{d'application}&&&\\\hline\vec{F}&&&&\\ \hline\end{array}$$
3. Tracer en rouge et nommer la zone de contact de :
 
3.1. la force qu'exerce le marteau sur le clou ;
 
3.2. la force qu'exerce le clou sur la planche ;
 
3.3. la force qu'exerce la planche sur l'établi

 
 

Exercice 4

On considère le dispositif de la figure ci-dessous
 
La masse de la bille est $m=75\;g$
 
1) Identifier les forces que subit la bille.
 
2) Préciser pour chaque force son auteur.
 
3) Donner les caractéristiques de chaque force.
 
4) dire à chaque fois s'il s'agit d'une force de contacte ou à distance, d'une force localisée ou répartie (Vous pouvez regrouper les réponses dans un tableau)
 
5) Représenter à l'échelle toutes ces forces.

 
 

Exercice 5

On considère le système de la figure ci-dessous, formé par un support $(S)$, un fil $(f)$, une boule $(B)$ et une règle en plastique dont on a frotté la partie présentée à la boule.
 
Sur cet ensemble on a représenté quelques forces. 
 
les points $I\;;\ J\ $ et $\ A$ sont des points d'attaches ou de contacts.

 

 
1) Compléter le tableau ci-dessous en procédant comme pour la première ligne.
 
2) Quelles sont les forces qui représentes une interaction ?
 
Écrire la relation vectorielle entre les forces de cette interaction.
 
3.a) La boule exerce-t-elle une force sur le fil ? Justifier.
 
b) Dans le cas d'une réponse positive, donner alors ses caractéristiques.
 
e) Représenter cette force.
$$\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline\vec{F}_{n}&\text{Auteur}&\text{Receveur}&\vec{F}_{.../...}&\text{Nature}&\text{Origine}&\text{Direction}&\text{Sens}&\text{valeur (N)}\\ \hline\vec{F}_{1}&S&F&\vec{T}_{s/f}&\text{de contact}&A&\text{celle du fil}&\text{vers le haut}&1\\ \hline&&&&&&&&\\ \hline&&&&&&&&\\ \hline&&&&&&&&\\ \hline&&&&&&&&\\ \hline&&&&&&&&\\ \hline&&&&&&&&\\ \hline\end{array}$$
 

Exercice 6

Soient deux forces $\vec{F}_{1}\ $ et $\ \vec{F}_{2}$ d'intensité $F_{1}=4\;N\ $ et $\ F_{2}=12\;N$
 
Représenter et déterminer par calcul l'intensité la résultante $\vec{F}$ des deux forces $\vec{F}_{1}\ $ et $\ \vec{F}_{2}$
 
1) $\vec{F}_{1}\ $ et $\ \vec{F}_{2}$ ont même direction et même sens
 
2) $\vec{F}_{1}\ $ et $\ \vec{F}_{2}$ ont même direction mais de sens opposés
 
3) $\vec{F}_{1}\ $ et $\ \vec{F}_{2}$ orthogonaux
 
4) $\vec{F}_{1}$ fait un angle $\alpha=30^{\circ}$ avec l'horizontal et dirigé vers haut et $\vec{F}_{2}$ angle $\beta=60^{\circ}$ avec la verticale et dirigé vers le bas
 

Exercice 7

1) Compléter les phrases suivantes à l'aide des mots de la liste ci-dessous :
 
Liste : Déformer, modifier, mouvement, mécanique, dynamomètre, mouvement, Newton, objet.
 
Une action ....... peut mettre en........
 
un......... Elle peut aussi........son......et/ou.......  cet objet.
 
L'intensité d'une force se mesure en........à l'aide d'un........
 
2) Rayer dans les phrases ci-dessous les mentions inutiles :
 
L'action du vent sur un drapeau est une action à distance /de contact.
 
L'action du stylo est une action ponctuelle /répartie.
 
L'action de la Terre sur un objet dans son voisinage est une action à distance /de contact.
 
L'action d'un aimant sur une bille métallique est une action à distance /de contact.
 
L'action de l'hameçon sur le poisson est une action ponctuelle /répartie.
 
L'action de ma main sur une poignée de porte est une action ponctuelle /répartie.
 
L'action des électrons sur le noyau de l'atome est une action à distance /de contact.
 
L'action d'un filin d'amarrage sur le bateau est une action ponctuelle /répartie.
 
L'action du pied sur le ballon est une action ponctuelle /répartie.
 

Exercice 8

1) Représenter la force exercée par le marteau sur le clou sachant qu'elle s'exerce au centre de la tête du clou, dans l'axe de celui-ci et d'une intensité de $150\;N.$
 
Échelle : $1\;cm$ pour $50\;N$

 

 
2) Un traîneau est tiré par deux chiens. Le chien 1 tire avec une force d'intensité $210\;N$ et le chien 2 avec une force d'intensité $180\;N.$
 
Construire les vecteurs forces $\vec{F}_{1}\ $ et $\ \vec{F}_{2}$ avec l'échelle $1\;cm\longrightarrow 60\;N$
 
Construire la somme $\vec{F}$ de ces 2 forces

 

 
Interprétation :
 
$-\ $ Pour avancer de la même façon avec un seul chien : Quelle doit-être l'intensité de la force exercée par ce chien ?
 
$-\ $ Le traîneau avance-t-il tout droit ? Si non, de quel côté dévie-t-il ?
 

Exercice 9

Un chariot est tiré par deux enfants. Chacun tire le chariot avec une force de valeur de $100\;N.$
 
L'angle de chacune des forces avec la direction de la route est $\alpha=20^{\circ}$
 
1) Citer deux méthodes pour déterminer la somme des deux forces $\vec{F}_{1}\ $ et $\ \vec{F}_{1}$
 
2) Déterminer la somme des deux forces $\vec{F}$ par une des méthodes à préciser

 

 
 

Exercice 10

1.1) Avec quel appareil mesure-t-on la valeur d'une force ?
 
1.2) Quel est l'unité légale de force ?
 
1.3) Quel est son symbole ?
 
2.1) Quelles sont les quatre caractéristiques d'une force ?
 
2.2) Par quoi est représentée une force ?
 

Exercice 11

Dire si les propositions suivantes sont vraies ou fausses. Corriger celles qui sont fausses.
 
1) Les actions de contact peuvent être ponctuelles ou réparties.
 
2) L'action du vent sur la voile du véliplanchiste est une action à distance.
 
3) L'unité légale de la force est le kilogramme, de symbole $kg.$
 
4) La valeur d'une force se mesure avec un dynamomètre.
 

Exercice 12

Décomposer les forces $\vec{P}\ $ et $\ \vec{T}$ suivant les directions indiquées. 
 
L'échelle est choisie de sorte que $1\;cm$ correspond à $5\;N$

 

 
 

Exercice 13

En exerçant des forces $F$ sur trois ressorts différents et en mesurant l'allongement $x$ des ressorts, on a obtenu les représentations graphiques.

 

 
1) Les trois ressorts vérifient-ils la loi de Hooke ? Comment le remarques-tu ?
 
2) Détermine les constantes de raideur des trois ressorts.
 
3) Quelle droite correspond au ressort le plus raide ? Justifie la réponse.

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$


 
 
Auteur: 
Sidy Mouhamed Ndiaye

Devoir n° 6 - Physique Chimie - 4e

Classe: 
Quatrième
 

Exercice 1

Complète les phrases suivantes :
 
Une réaction qui s'accompagne d'un dégagement de chaleur est dite$\ldots\ldots$
 
On fait réagir de l'acide chlorhydrique $HCl$ sur l'aluminium $Al.$
 
Il se forme du chlorure d'aluminium $AlCl_{3}$ et du dihydrogène $H_{2}.$
 
Dans cette réaction chimique, les réactifs sont$\ldots\ldots$et$\ldots\ldots$
 
Les produits de la réaction sont$\ldots\ldots$et$\ldots\ldots$
 

Exercice 2

1) Équilibrer les équations des réactions suivants :
$$N_{2}\quad +\quad H_{2}\quad\longrightarrow\quad NH_{3}$$
$$C\quad +\quad O_{2}\quad\longrightarrow\quad CO$$
2) Le carbone réduit l'oxyde ferrique $(Fe_{2}O_{3})$ selon l'équation bilan suivante :
$$2Fe_{2}O_{3}\quad +\quad 3C\quad\longrightarrow\quad Fe\quad +\quad 3CO_{2}$$
On procède à la réduction de $80g$ d'oxyde ferrique.
 
a) Calcule la masse molaire moléculaire du dioxyde ferrique réduit.
 
b) Calcule la quantité de matière de l'oxyde ferrique réduit.
 
c) Calcule la masse de fer formé.
 

Exercice 3

Mme FAYE voudrait savoir si ses cuillères sont en or massif, c'est-à-dire en or pur.
 
Elle recherche la masse volumique de l'or et trouve $\rho_{\text{or}}=19.3\;g.ml^{-1}$.
 
Elle mesure ensuite le volume et la masse d'une de ses cuillères par la méthode ci-dessous.

 

 
1) Quelle est le volume de la cuillère ?
 
2) Quelle est la masse de la cuillère ?
 
3) Restitue la définition de la masse volumique d'un corps.
 
4) Détermine la masse volumique de cette cuillère utilisée.
 
5) Quelle conclusion peut tirer Mme FAYE.
 

Exercice 4

Un objet en aluminium a une masse $1.35\;kg$
 
1) Calcule son poids sur terre sachant $g=10\;N.kg^{-1}$
 
2) Représente vectoriellement le poids de cet objet à l'échelle de $1\;cm$ pour $6.75\;N$.
 
3) Donne les caractéristique de ce poids de cet objet.
 
4) Quelle serait la masse de cet objet s'il était transporté sur la planète mercure ?
 
 
$$\text{Durée 1h 30}$$
Auteur: 
Aliou ndiaye

Pages