Physique

Série d'exercices : Mouvement d'une particule chargée dans un champ magnétique uniforme - Ts

Classe: 
Terminale
 

Exercice 1

1) On considère les ions de deux isotopes de mercure $_{80}^{200}Hg^{2+}$ et $_{80}^{202}Hg^{2+}$ de masses respectives $m_{1}=3.32\cdot10^{-25}kg$ et $m_{2}=3.35\cdot10^{-25}kg$ et de même charge $q=2e.$ 
 
Ils sont ensuite émis sans vitesse par la source $S$, puis accélérés par un champ électrostatique uniforme qui règne entre $S$ et $P$ tel que $U_{SP}=U=600V.$ 
 
 
 
a) Déterminer l'expression littérale de la vitesse $\|\overrightarrow{V}\|$ en $A$ d'un ion de masse $m$ et de charge $q$ en fonction de $m$, $e$ et $U.$
 
b) Montrer que les deux ions $_{80}^{200}Hg^{2+}$ et $_{80}^{202}Hg^{2+}$ émis par $S$ arrivent en $A$ avec des vitesses différentes.
 
2) Ces deux ions pénètrent en $A$ dans une région où règne un champ magnétique uniforme $\overrightarrow{B}$ perpendiculaire au plan de la figure et tel que $\|\overrightarrow{B}\|=0.2T$ qui leur impose une trajectoire circulaire de rayon $R$, puis ils impressionnent une plaque photographique en deux points $I$ et $F.$
 
a) Établir l'expression de $R$ en fonction de $m$, $e$, $\|\overrightarrow{B}\|$ et $\|\overrightarrow{V}\|$ puis en fonction de $m$, $e$, $\|\overrightarrow{B}\|$ et $U.$
 
b) Calculer $R_{1}$ et $R_{2}$ et déduire la distance $IF$ entre les deux points d'impact, sur la plaque photo des ions des deux isotopes de mercure $Hg^{2+}$

Exercice 2

Un cyclotron est un instrument qui sert à accélérer des particules chargées, permettant ensuite de réaliser des expériences de physique nucléaire. 
 
Dans ce problème les particules chargées sont des protons de masse $m_{p}=1.67\cdot10^{-27}kg$ et de charge électrique $q_{p}=+1.6\cdot10^{-19}C$
 
Le cyclotron est formé de deux demi-cylindres conducteurs creux appelés « dees » et séparés par un intervalle étroit. 
 
Un champ magnétique uniforme $B$ règne à l'intérieur de chaque « dee », sa direction est parallèle à l'axe de ces demi-cylindres, sa valeur est $1.0T.$
 
Un champ électrique $E$ variable dans le temps, peut être établi dans l'intervalle étroit qui sépare les « dees ». 
 
Il permet d'augmenter la vitesse des protons chaque fois qu'ils pénètrent dans cet intervalle.
 
Ce champ électrique variable est obtenu en appliquant une tension sinusoïdale de valeur maximale $U_{M}$ et de fréquence $f$ entre les deux « dees »: $U_{M}=2\cdot10^{3}V$
 
 
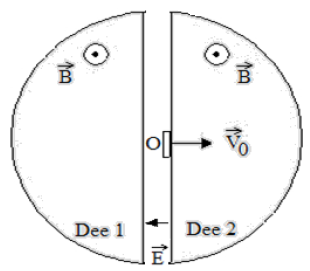
1. Le proton entre dans le « dee » $1$ avec une vitesse initiale d'injection $V_{0}$ perpendiculaire à l'axe des demi-cylindres. 
 
On négligera le poids du proton devant la force magnétique.
 
1.1 Donner l'expression de la force agissant sur le proton en $O$ ; la représenter sur un schéma
 
1.2 Le mouvement du proton étant plan, montrer que la valeur de la vitesse est constante.
 
1.3 Montrer que la trajectoire est circulaire de rayon $R_{0}=\dfrac{m_{p}}{q_{pB}}V_{0}$
 
2.1 Exprimer la longueur parcourue par un proton sur le demi-tour de rayon $R_{0}.$
 
2.2 En déduire l'expression du temps $t$ mis par ce proton pour effectuer ce demi-tour.
 
2.3 Ce temps dépend-il de la vitesse d'entrée du proton dans le « dee » ? 
 
Calculer la valeur de $t.$
 
3. Le proton, après avoir fait un demi-cercle dans un « dee », entre dans l'intervalle étroit où il est accéléré par le champ électrique considéré comme constant, maximum et colinéaire au vecteur vitesse du proton durant son passage.
 
Calculer la fréquence $f$ de la tension alternative appliquée entre les « dees » pour que les protons subissent une accélération maximale à chaque traversée de l'intervalle. 
 
On suppose que le temps de traversée de l'intervalle est négligeable devant le temps passé dans les « dees ».
 
4.1 Exprimer littéralement, puis calculer la variation d'énergie cinétique $\Delta\,Ec$ du proton lorsqu'il traverse l'intervalle étroit. 
 
Le résultat sera exprimé en joule puis en électron-volt.
 
4.2 Préciser si le rayon de la trajectoire du proton augmente ou diminue à chaque fois qu'il traverse l'intervalle étroit (justifier la réponse)
 
5. La vitesse d'injection du proton étant supposée pratiquement nulle, on désire que sa vitesse atteigne $2\cdot10^{4}km\cdot s^{-1}$
 
Calculer le nombre de tours que le proton devra décrire dans le cyclotron.
 
6. Calculer la valeur du rayon à partir duquel les protons ayant acquis une vitesse de $2\cdot10^{4}km\cdot s^{-1}$ seront extraits, en admettant qu'ils sont injectés à proximité immédiate du centre $O$ du cyclotron

Exercice 3 : Utilisation d'un spectrographe de masse 

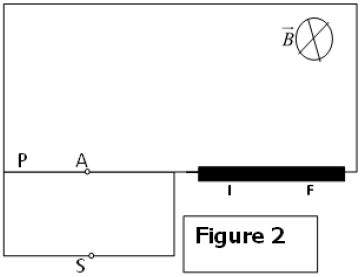
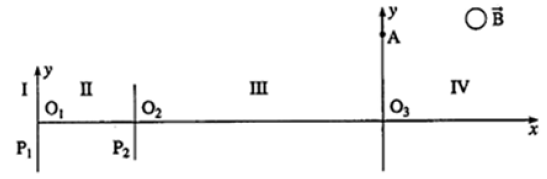
Sur le schéma ci-dessous, on retrouve la même zone $I$ d'ionisation fournissant les ions $X^{+}.$ 
 
On a ensuite la zone $II$ où on applique une tension accélératrice : $U'=8.00\,kV$ entre les plaques $P_{1}$ et $P_{2}$ permettant de donner aux ions $X^{+}$ une vitesse $v'.$ 
 
Dans la zone $III$ un dispositif de filtrage permet d'éliminer les éventuelles particules parasites qui auraient pu être obtenues par fragmentation des molécules $X$ lors de l'ionisation par choc électronique. 
 
Enfin dans la zone $IV$ existe un champ magnétique de direction orthogonale au plan de figure et de norme : $B=1.80T.$ 
 
L'ion $X^{+}$, animé de la vitesse $v'$ pénètre en $O_{3}$ dans cette zone suivant l'axe $O_{3}x.$
 
 
1) Rappeler l'expression de la force magnétique s'exerçant sur l'ion $X^{+}.$ 
 
Représenter sur un schéma le vecteur force pour que la déviation à partir de $O_{3}$ se fasse du côté positif de l'axe $O_{3}y.$ 
 
En déduire le sens du vecteur champ magnétique.
 
2) Démontrer que le mouvement de l'ion $X^{+}$ dans la zone $IV$ est plan et uniforme.
 
3) Montrer que l'ion $X^{+}$ décrit dans cette zone un arc de cercle, dont on établira l'expression littérale du rayon en fonction de $m$, $e$, $v'$ et $B.$
 
4) Exprimer le rayon du cercle trajectoire en fonction de $U'$, $m$, $e$ et $B.$
 
5) L'ion $X^{+}$ est recueilli au point $A$ tel que : $O_{3}A=0.069\,m.$
 
Trouver la masse de l'ion $X^{+}$ et identifier la substance $X.$

Exercice 4 : spectromètre de masse

Une source radioactive ponctuelle émet, suivant un axe $Ox$, un faisceau de particules passant entre les plaques horizontales d'un condensateur plan. 
 
L'action de la pesanteur est négligeable devant celle de la force de Lorentz. 
 
En l'absence de tout champ, les particules frappent en $O$ un écran situé à la distance a de la sortie du condensateur. 
 
On soumet alors le faisceau à un champ électrique uniforme et vertical $\overrightarrow{E}$, créé par le condensateur, et à un champ magnétique, uniforme, horizontal, perpendiculaire à l'axe $Ox$ et dirigé d'avant $\overrightarrow{B}$ en arrière.
 
 
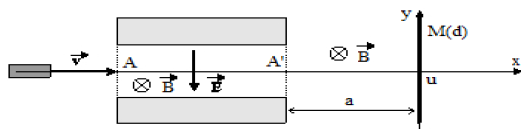
a) Les particules entrent en $A$ dans le condensateur avec une vitesse parallèle à $Ox.$ 
 
Quelle doit être la valeur du champ $\overrightarrow{E}$ pour que les particules ne soient pas déviées ? 
 
Que se passe-t-il si $q$ change de signe ?
 
b) Le faisceau horizontal et monocinétique sortant en $A'$ du condensateur, est ensuite soumis à la seule action du champ magnétique et vient frapper l'écran au point $M$ tel que $OM=d.$
 
i) Montrer que les particules de même rapport $q/m$ décrivent des trajectoires circulaires uniformes de même rayon $R.$ 
 
Calculer $R.$ 
 
Quel effet a le signe de $q$ sur la déviation ?
 
ii) Montrer que $R=(d^{2}+a^{2})/2d.$ 
 
En déduire la valeur de $q/m.$
 
c) A.N. : on détecte des particules pour la valeur suivante des champs et de la déviation $d$ : $B=0$, $32T$ $E=6.4\cdot10^{6}Vm^{-1}$ ; $a=50\,cm$, $d=10\,cm$ vers le haut. 
 
Identifier ces particules sachant que pour l'électron $e=1.6\cdot10^{-19}C$, $m_{e}=9.1\cdot10^{-31}Kg$ et pour le proton et le neutron $m_{p}=m_{n}=1830\,m_{e}$

Exercice 5

Une particule de charge $q$, de masse $m$ traverse une chambre de Wilson dans laquelle règne un champ magnétique $B$ uniforme perpendiculaire au plan de la figure et orienté vers l'avant de ce plan. 
 
La particule ralentit en franchissant la surface $AB.$
 
Le cliché matérialisant la trajectoire permet de dire que la particule décrit des arcs de cercles de rayons $r_{1}$ et $r_{2}$ respectivement dans les parties $I$ et $II.$
 
 
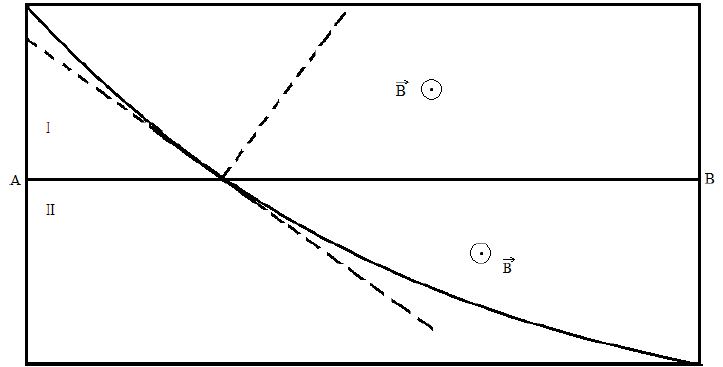
1. Établir l'expression de $r_{1}$ et $r_{2}$ en fonction de $q$, $m$, $B$ et des vitesses respectives $v_{1}$ et $v_{2}$ de la particule. 
 
Dans quel sens se déplace la particule $($de $I$ vers $II$ ou de $II$ vers $I)$ ?
 
On donne : $r_{1}=\dfrac{r_{2}}{3}=14\,cm$
 
2. Quel est le signe de la particule ? 
 
Justifier la réponse
 
3. Calculer la charge massique $\dfrac{q}{m}$ et identifier la particule
 
On donne : 
 
$B=0.50T$ ; 
 
$v=2.0\cdot10^{7}m\cdot s^{-1}$ ; 
 
$m_{e}=9.1\cdot10^{-31}Kg$ ;
 
$m_{p}=1.67\cdot10^{-27}Kg$ ; 
 
$e=1.6\cdot10^{-19}C$

Exercice 6

Dans tout le problème, on négligera le poids de la particule devant les autres forces et on appliquera les lois de la mécanique classique
 
On envisage la séparation d'isotopes du Xénon $(Xe)$ au moyen d'un spectrographe de masse
 
Une chambre d'ionisation produit des ions positifs $_{54}^{129}Xe^{+}$ et $_{54}^{x}Xe^{+}.$ 
 
Ces ions sont ensuite accélérés entre deux plaques métalliques parallèles $P_{1}$ et $P_{2}$, puis à l'action d'un champ magnétique permet de les séparer
 
On donne : 
 
$e=1.6\cdot10^{-19}C$, 
 
$m_{n}=m_{p}=1.67\cdot10^{27}Kg$
 
 

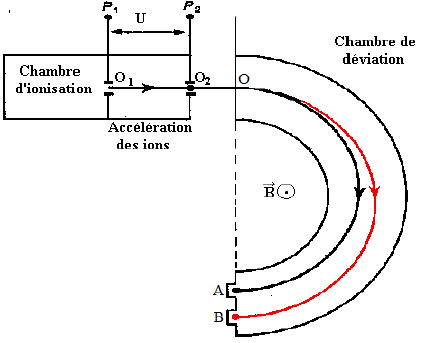
1. Accélération des ions

Les ions traversent la plaque $P_{1}$ en $O_{1}$ sans vitesse initiale. 
 
Ils sont alors soumis entre $P_{1}$ et $P_{2}$ à une accélératrice $U=1000V$
 
a) Dans quel sens cette tension doit-elle être établie
 
b) Montrer que l'énergie cinétique, acquise par les ions lorsqu'ils traversent la plaque $P_{1}$ en $O_{1}$, est indépendante de l'isotope envisagé et cette valeur en joules
 
c) Calculer la vitesse acquise par les ions $_{54}^{129}Xe^{+}$ en $O_{2}.$
 
On assimilera la masse de l'ion à la somme des masses de ses nucléons
 
d) Exprimer en fonction de $x$ et $v$, la vitesse $v'$ acquise par les ions $_{54}^{x}Xe^{+}$ en $O_{2}$

2. Séparation des ions

Les ions, animés des vitesses $v$ et $v'$, pénètrent en $O$ dans une région où règne un champ magnétique $\overrightarrow{B}$ uniforme perpendiculaire au plan de la figure
 
a) On s'intéresse au mouvement des ions $_{54}^{129}Xe^{+}.$ 
 
Montrer que celui-ci est plan, circulaire et uniforme. 
 
Donner l'expression du rayon de courbure $R.$ 
 
Calculer $R$ pour $B=0.1T$
 
Les ions $_{54}^{129}Xe^{+}$ et $_{54}^{x}Xe^{+}$ décrivent un demi-cercle avant de tomber sur plaque photographique, respectivement en $A$ et $B$
 
b) On mesure la distance $AB=8\,cm.$ 
 
En déduire la valeur de $x\ (B=0.1T)$

Exercice 7

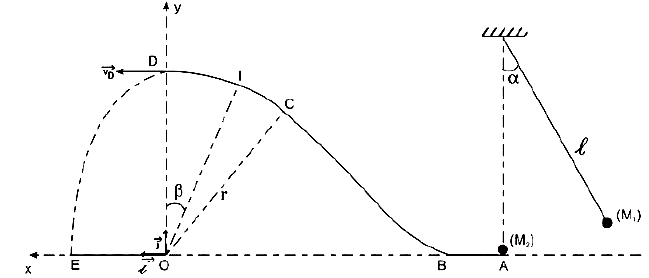
Pour identifier des ions désignés par $X_{1}$ ; $X_{2}$ ; $X_{3}$ et $X_{4}$, portant chacun une charge de valeur absolue $|q|=e$ on les introduit successivement dans une région où règne un champ magnétique $B$ uniforme avec la même vitesse $v_{0}.$ 
 
Les trajectoires obtenues sont représentées sur la figure suivante
 
 
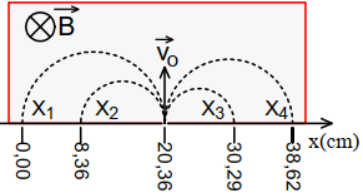
1. Montrer que le mouvement d'une particule de masse $m$ et de charge $q$ de vitesse initiale $v_{0}$ perpendiculaire au vecteur champ magnétique uniforme $B$ est un mouvement uniforme circulaire. 
 
Puis montrer que : $$R=\dfrac{mV_{0}}{|q|B}$$
 
Donnée : 
 
la masse de l'ion d'un élément $^{A}X$ est : $m=Au$
 
2. En exploitant la figure :
 
2.1 Identifier le signe de la charge portée par chacun des ions $X_{1}$ ; $X_{2}$ ; $X_{3}$ et $X_{4}$ ?
 
2.2 Déterminer les rayons $R_{1}$ ; $R_{2}$ ; $R_{3}$ et $R_{4}$ de ces ions.
 
3. Identifier les ions $X_{1}$ ; $X_{2}$ ; $X_{3}$ et $X_{4}$ dans la liste suivante : 
 
$^{39}K^{+}$ ; $^{23}Na^{+}$ ; $^{35}Cl^{-}$ ; $^{19}F^{-}.$

Exercice 8

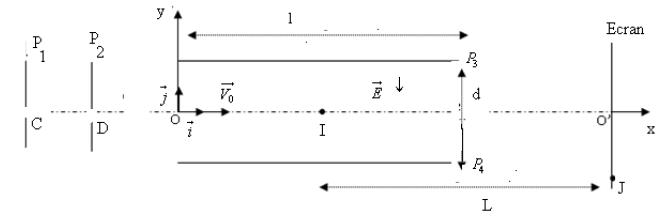
Un faisceau d'électrons émis par une cathode pénètre par le point $A$ de coordonnées $x_{A}=-0.20(m)$ ; $y_{A}=0$ avec une vitesse $\overrightarrow{V}_{0}=V_{0}\vec{j}$ dans une région où règne un champ magnétique uniforme $\overrightarrow{B}$ normal au plan $(Oxy)$ ou s'effectue le mouvement.
 
L'électron quitte le champ magnétique en $C$ avec une vitesse $\overrightarrow{V_{C}}$ pour aborder une zone où règne un champ électrostatique uniforme $\overrightarrow{E}$ pour en sortir au point $D$ de coordonnées $x_D=+0.20(m)$ ; $y_{D}=0$ avec une vitesse $\overrightarrow{V_{D}}$
 
1. Étude du mouvement de l'électron dans le champ $\overrightarrow{B}$
 
1.1 En appliquant la deuxième loi de Newton montrer que :
 
$-\ $ Le mouvement de l'électron est uniforme 
 
$-\ $ Le mouvement de l'électron est circulaire  
 
1.2 Donner l'expression du rayon $R$ de la trajectoire de l'électron 
 
1.3 Calculer la valeur de l'intensité de $\overrightarrow{B}$
  
1.4 Déterminer la durée  du mouvement de l'électron dans cette zone 
 
 
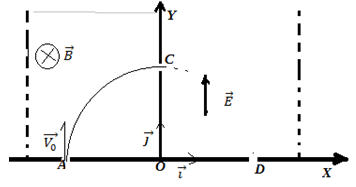
2. Étude du mouvement de l'électron dans le champ $\overrightarrow{B}$
 
On prend comme origine des dates $(t=0)$ l'instant d'arrivée de l'électron au point $C$
 
2.1 En appliquant la deuxième loi de Newton :
 
$-\ $ Établir les équations horaires du mouvement de l'électron 
 
$-\ $ En déduire l'équation de la trajectoire dans le repère $(O\;,\ \vec{i}\;,\ \vec{j})$
 
2.2 Calculer la valeur de l'intensité de $\overrightarrow{E}$
  
2.3 Déterminer la durée  du mouvement de l'électron dans cette zone 
 
Les données : on néglige l'effet du champ de pesanteur sur l'électron ; la charge de l'électron
 
$-e=-1.6\cdot10^{-19}C$ ; $V_{0}=10^{7}m\cdot s^{-1}$ ;
 
la masse de l'électron : $m=9.1\cdot10^{-31}kg$ ; les directions de $\overrightarrow{V_{0}}$ et celle de $\overrightarrow{V_{C}}$ font un angle de $\dfrac{\pi}{2}$ radian ; le repère $(O\;,\ \vec{i}\;,\ \vec{j})$ est orthonormé

Exercice 9

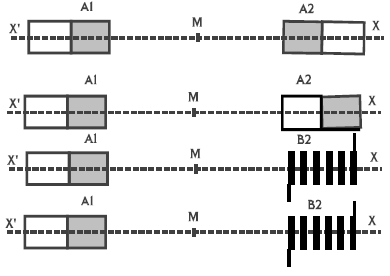
Le spectrographe de masse est un dispositif utilisé pour la séparation des isotopes. 
 
Il est constitué :
 
$-\ $ d'une chambre (1) d'ionisation dans laquelle sont ionisés les isotopes à séparer,
 
$-\ $ d'une chambre (2) d'accélération des ions dans laquelle règne un champ électrique uniforme $\overrightarrow{E}$ créé par une tension $U_{0}$ appliquée entre deux plaques $(P_{1})$ et $(P_{2})$,
 
$-\ $ d'une chambre (3) hémicylindrique dans laquelle règne un champ magnétique uniforme $\overrightarrow{B}$,
 
$-\ $ d'un détecteur d'ions.
 
On se propose de séparer des isotopes de l'élément chlore.
 
On négligera dans tout l'exercice, le poids de l'ion chlorure devant les autres forces qui interviennent
 
 
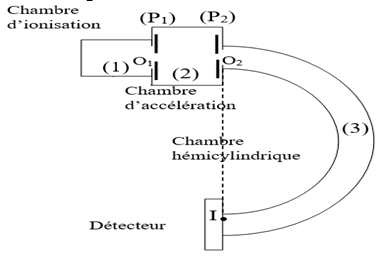
1) a) Préciser le sens de pour que des ions négatifs, sortant de la chambre d'ionisation en $O_{1}$ avec une vitesse nulle, aient, dans la chambre d'accélération, un mouvement rectiligne accéléré suivant la direction $O_{1}O_{2}$ ? 
 
Justifier la réponse. 
 
b) Montrer qu'au point $O_{2}$, l'énergie cinétique est la même pour les différents types d'ions accélérés qui correspondent au même élément chimique et qui portent la même charge électrique. 
 
En est-il de même pour les vitesses ? 
 
Justifier la réponse.
 
2) Dans la chambre (3) règne un champ magnétique $\overrightarrow{B}$ normal au plan contenant $O_{1}$, $O_{2}$ et $I.$ 
 
Préciser son sens pour que des ions négatifs soient déviés vers un point d'impact $I$ du détecteur. 
 
3) Préciser la nature du mouvement d'une particule chargée dans chacune des chambres (2) et (3). 
 
4) Des ions chlorure $Cl^{-}$ sont accélérés sous une tension $U_{0}=500V.$
 
a) Déterminer l'intensité du champ magnétique $\overrightarrow{B}$ qui doit régner dans la chambre (3) pour que des ions $^{35}Cl^{-}$ viennent frapper le détecteur au point d'impact $I$ situé à $19cm$ de $O_{2}.$
 
b) Au niveau du détecteur et en un point $I'$ situé plus loin que $I$ du point $O_{2}$, on reçoit des ions négatifs désigné par $^{A}Cl^{-}.$ 
 
Sachant que la distance qui sépare le point $I$ du point $I'$ est $0.6cm$, déterminer le nombre de masse de l'ion $^{A}Cl^{-}$ considéré. 
 
c) Répondre par vrai ou faux aux propositions suivantes :
 
Dans un champ électrique uniforme, une particule chargée mobile suit toujours une trajectoire rectiligne.
 
Dans un champ magnétique uniforme, une particule chargée mobile suit toujours une trajectoire circulaire.
 
Développer, dans chaque cas, ce qui justifie la réponse.
 
On donne : 
 
Charge électrique élémentaire : $e=1.6\cdot10^{-19}C$ ; Unité de masse atomique : $u=1.66\cdot10^{-27}kg$

Exercice 10

Une particule injectée au cœur du cyclotron va être accélérée par le champ électrique alternatif de haute fréquence entre les « dés ». 
 
Puis, elle entre dans le « dé » suivant lorsque le champ électrique change de sens et elle est donc à nouveau accélérée, et ainsi de suite 
 
Sa trajectoire devient plus périphérique du fait de son augmentation d'énergie. 
 
Elle sera éjectée de l'accélérateur avec l'énergie adéquate à partir de cette dernière trajectoire, puis guidée et focalisée jusqu'à sa cible. 
 
1. Représenter, en justifiant, au point $A$ de la trajectoire de l'ion injecté dans le cyclotron, le vecteur vitesse $\overrightarrow{v}$ de l'ion et la force magnétique $\overrightarrow{F_{m}}$ qui s'exerce sur l'ion. 
 
Représenter le champ magnétique, $\overrightarrow{B}$ dans l'hypothèse où la charge $q$ de l'ion est positive. 
 
2. Montrer que l'action du champ $\overrightarrow{B}$ ne permet pas d'accroître l'énergie cinétique de l'ion. 
 
3. Démontrer que dans un $« D »$, dans l'hypothèse où le champ magnétique est uniforme et constant, le mouvement de l'ion est circulaire uniforme et exprimer le rayon de la trajectoire en fonction de $m$ (masse de l'ion), $v$ (module de la vitesse de l'ion), $q$ et $B.$
 
4. Montrer que la durée de passage dans un demi-cylindre, notée $t_{p}$ ne dépend pas de $v.$
 
Pour accroître l'énergie cinétique de l'ion, on utilise l'action du champ électrique $\overrightarrow{E}$ résultant de la tension $u$ appliquée entre les deux $« D ».$ 
 
On considère que pendant la durée très courte de passage de l'ion d'un $« D »$ à l'autre, la tension $u$ reste constante. 
 
5. Déterminer, en fonction de $q$ et $u$ les expressions des variations de l'énergie cinétique de l'ion lors de la traversée de l'espace entre les deux $« D ».$
 
6. Un ion est injecté dans la zone d'accélération avec une vitesse nulle. 
 
Quelle est sa vitesse $v_{1}$ au moment de la pénétration dans le premier $« D »$ et quel est le rayon $R_{1}$ de la première trajectoire semi-circulaire ? 
 
7. On peut négliger la durée de passage de l'ion dans l'intervalle entre les deux $« D »$ devant la durée de passage de l'ion dans un demi-cylindre. 
 
La tension $u$ est une fonction sinusoïdale du temps qui doit être synchronisée avec le mouvement des particules chargées de telle sorte que le champ électrique soit inversé à chaque demi-tour. 
 
Quelle doit être la fréquence d'oscillation de cette tension $u(t)$ permettant d'obtenir une accélération de l'ion à chaque passage dans l'intervalle entre les deux $« D ».$
 
8. Après chaque passage dans l'intervalle entre les deux $« D »$, la vitesse de la particule ainsi que le rayon $R$ de sa trajectoire dans un $« D »$ augmentent. 
 
Déterminer les suites $v_{k}$ et $R_{k}$, l'indice $k$ étant incrémenté d'une unité à chaque demi-tour.
 
9. Lorsque ce rayon finit par atteindre le rayon $R_{D}$ d'un $« D »$, l'ion est alors éjecté du cyclotron.
 
Exprimer en fonction de $m$, $q$, $B$ et $R_{D}$ l'énergie cinétique $E_{k}$ de l'ion lors de son éjection. 
 
10. Application numérique. 
 
Calculer, en joule, puis en $MeV$, l'énergie cinétique $E_{k}$ d'un ion zinc $Zn^{11+}$ sachant que : 
 
$B=1.67T$ ; $m=1.06\cdot10^{-25}kg$ ; $R_{D}=0.465m$ ; $e=1.60\cdot10^{-19}C$
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Série d'exercices : Généralité sur les champs magnétiques - Champs magnétique des courants - Ts

Classe: 
Terminale
 

Exercice 1

1) Représenter le spectre de l'aimant représenté ci-dessous.
 
 
2) On place au point $A$ un capteur de champ magnétique, de sensibilité : $20\,mV/mT.$
 
Celui-ci indique $227\,mV.$
 
a) Calculer l'intensité du champ magnétique au point $A.$
 
b) Tracer le vecteur champ magnétique en ce point.

Exercice 2

1) Tracer le spectre de l'aimant en $U$ entre les deux pôles.
 
 
2) Orienter les lignes de champ.
 
3) Identifier les pôles de cet aimant.
 
4) Quelle propriété possède le vecteur $B$ dans cette région de l'espace champ magnétique ?
 
Comment appelle-t-on un tel champ magnétique ?

Exercice 3

Soit un solénoïde de longueur $L=50\,cm$, constitué de $2000$ spires et parcouru par un courant d'intensité $1.5\,A.$
 
1) Identifier les pôles de ce solénoïde.
 
2) Calculer la norme du champ magnétique créé au centre de ce solénoïde.
 
3) Représenter le vecteur champ magnétique en ce point.
 
4) La norme du champ en $A$ est de $0.5\,mT.$
 
Représenter le vecteur champ magnétique en $A.$
 
 

Exercice 4

Deux aimants droits $A_{1}$ et $A_{2}$ sont placés sur l'axe $x'x.$ 
 
 
Chacun d'eux crée au point $M$ situé à égale distance des deux sources, un champ magnétique de $20\,mT.$
 
1) Représenter le vecteur champ magnétique en $M$, lorsque les deux pôles en regard sont de même nom.
 
2) Même question lorsque les deux pôles sont de noms différents.
 
3) On remplace l'aimant $A_{2}$ par une bobine $B_{2}.$
 
On désire qu'au point $M$ le champ résultant ait une norme égale à $60\,mT.$
 
Quelle doit être la norme du champ magnétique créé par la bobine ? 
 
(Deux cas sont envisageables).
 
Pour chaque cas, quel est le sens du courant dans la bobine ?

Exercice 5

 
Une bobine parcourue par un courant d'intensité $I$, crée en $M$ un champ magnétique de norme $B_{1}=2\,mT.$
 
Un aimant $A$ crée en $M$ un champ magnétique de norme $B_{2}=4\,mT.$
 
1) Représenter les vecteurs champ magnétique créés en $M$ par chacune des deux sources.
 
2) Représenter le vecteur champ magnétique résultant.
 
Déterminer sa norme.

Exercice 6

A l'intérieur d'un solénoïde $S_{1}$ comportant $n_{1}$ Spires par mètre, parcouru par un courant d'intensité $I_{1}$, on place un solénoïde $S_{2}$ dont l'axe est orthogonal à celui de $S_{1}$, comportant $n_{2}$ spires par mètre et parcouru par un courant $I_{2}.$
 
 
1) $I_{2}=0$ ; Représenter le vecteur induction magnétique $B_{1}$ au centre de $S_{1}$ et exprimer son intensité en fonction de $n_{1}$ et $I_{1}.$
 
2) $I_{2}\neq 0$ ; indiquer en le justifiant, le sens de $I_{2}$ pour que le vecteur induction $B_{2}$ crée au centre de $S_{2}$ ait le même sens que l'axe $(y'y).$
 
3) Une petite aiguille aimantée, placée au centre $O$ des deux solénoïdes prend une direction $\alpha$ avec l'axe $(x'x).$
 
a) Faire un schéma clair dans lequel sont représentés les vecteurs $B_{1}$, $B_{2}$ et l'aiguille.
 
b) Exprimer le rapport $n_{2}/n_{1}$ en fonction de $\alpha$, $I_{1}$ et $I_{2}.$
 
c) Calculer $n_{1}$ et $n_{2}$ sachant que $n_{1}+n_{2}=500\text{spires}\cdot m^{-1}.$ 
 
On donne $\alpha=63.2^{\circ}$ ; 
 
$I_{1}=2A$ et $I_{2}=1A.$
 
En déduire la valeur du champ résultant en $O.$

Exercice 7

La valeur de la composante horizontale du champ géomagnétique étant trop faible pour être mesurée à l'aide d'un tesla mètre courant, on se propose de la déterminer de la manière suivante.
 
On place une aiguille aimantée sur pivot vertical au centre $O$ d'un solénoïde long, à spires non jointives comportant $n=200$ spires par mètre, de manière à pouvoir observer l'orientation de l'aiguille. 
 
Le solénoïde est alors disposé horizontalement, et orienté pour que son axe soit perpendiculaire à celui de l'aiguille aimantée. 
 
On alimente le solénoïde avec un courant d'intensité suffisante pour produire un champ magnétique en $O$ de valeur $B_{S}.$ 
 
On constate que l'axe de l'aiguille aimantée est dévié d'un angle $\alpha.$
 
1) Indiquer sur le schéma suivant l'orientation de la boussole placée au point $O$ en absence de courant.
 
 
2) Représenter sans souci d'échelle sur le schéma ci-dessous, le vecteur $\overrightarrow{B_{S}}$ du champ magnétique crée par le courant électrique $i$ au centre $O$ du solénoïde. 
 
En déduire les faces nord et sud du solénoïde.
 
 
3) Une étude expérimentale consiste à mesurer la valeur de la déviation $\alpha$ de l'aiguille aimantée placée en $O$, pour différentes valeur de l'intensité du courant $i$ qui circule dans le solénoïde.
 
Les résultats obtenus ont permis de tracer la courbe ci-dessous.
 
 
a) Déterminer l'équation numérique de la courbe $\tan\alpha=f(i).$
 
b) Faire un schéma sur lequel on représentera les vecteurs $B_{H}$ et $B_{S}$ (sans souci d'échelle) au point $O.$
 
c) Trouver une relation entre la valeur de $B_{H}$ et $B_{S}$ et $\alpha.$
 
4) En déduire la valeur de la composante horizontale $B_{H}$ du champ géomagnétique.

Exercice 8

On dispose d'un solénoïde de longueur $L=40\,cm$ et comportant $N=250$ spires. 
 
On le place de telle sorte que son axe soit horizontal et perpendiculaire au plan du méridien magnétique. 
 
Le solénoïde est parcouru par un courant électrique d'intensité constante.

Partie I

Le champ magnétique terrestre peut être négligé.
 
On effectue des mesures de la valeur $BS$ du champ magnétique $B_{S}$ à l'intérieur du solénoïde. 
 
La sonde est placée sur l'axe du solénoïde à une distance $x$ de son centre $O.$ 
 
On obtient les résultats suivants :
$$\begin{array}{|c|c|c|c|c|c|c|c|} \hline x(cm)&0&4&8&11&14&17&20\\ \hline B_{S}(mT)&3.3&3.3&3.3&3.3&3.2&2.8&2.1\\ \hline \end{array}$$
 
1) Tracer un graphique représentant les variations de $B$ en fonction de $x$ sur toute la longueur du solénoïde.
 
2) Que peut-on dire du champ magnétique à l'intérieur de la bobine ?
 
3) Calculer l'intensité $I$ du courant qui traverse la bobine.
 
4) A l'aide du graphique, déterminer la longueur du solénoïde sur laquelle la valeur du champ magnétique reste supérieure à $90\%$ de sa valeur maximale.

Partie II

On fait maintenant diminuer l'intensité du courant dans les spires du solénoïde afin que la composante horizontale du champ magnétique terrestre ne soit plus négligeable. 
 
On a $I=0.1\,A.$
 
On place au centre de la bobine une petite aiguille aimantée. 
 
Celle-ci s'oriente spontanément dans une direction faisant un angle $\alpha=14.3^{\circ}$ avec l'axe du solénoïde.
 
1) On veut que le champ $B_{S}$ crée par la bobine soit dirigé vers la droite. 
 
Indiquer quel doit être le sens du courant dans les spires pour que ce soit effectivement le cas.
 
2) Faire un schéma représentant les vecteurs champs créés par le solénoïde $B_{S}$ et par la Terre $B_{H}$, ainsi que le champ résultant $B.$
 
3) Calculer la nouvelle valeur de $B_{S}.$

Exercice 9

1) Calculer l'intensité du champ magnétique $\overrightarrow{B}$ créé au point $M$ par les courants $I_{1}$ et $I_{2}$ qui traversent respectivement les fils rectilignes considérés comme infiniment longs. 
 
On donne : 
 
$I_{1}=I_{2}=I=6.0\,A$ et $d=12\,cm$
 
2) On néglige le champ magnétique terrestre. 
 
On place une petite aiguille aimantée au point $O$ ? 
 
Quelle orientation prend-elle ?
 
(Choisir ci-dessous la bonne réponse en justifiant la réponse)
 
 
Deux solénoïdes $(S_{1})$ et $(S_{2})$ comportant respectivement $n_{1}=400$ spires par mètre et $n_{2}=80$ spires par mètre, sont disposés de manière à avoir le même axe ; cet axe commun étant perpendiculaire au plan du méridien magnétique terrestre (figure ci-dessous).
 
On place un l'aiguille aimantée mobile autour d'un axe vertical, à l'intérieur des deux solénoïdes qu'on branche en série dans un circuit électrique. 
 
Lorsque le courant continu qui parcourt les deux solénoïdes a une intensité $I$, l'aiguille aimantée dévie de l'angle $\alpha=45^{\circ}.$
 
 
Déterminer la valeur de l'intensité $I.$ 
 
On distinguera le cas où la borne $(A_{1})$ est reliée à la borne $(B_{2})$ puis le cas où la borne $(A_{1})$ est reliée à la borne $(A_{2})$

Exercice 10

On étudie expérimentalement, à l'aide d'un teslamètre, l'intensité $B$ du champ magnétique à l'intérieur d'une bobine parcourue par un courant, en fonction de différents paramètres.
 
La bobine comporte $200$ spires, est longue de $40.0\,cm$, et a un diamètre de $5.0\,cm.$

I. Introduction

1. Décrire une méthode permettant de visualiser les lignes de champ de la bobine.
 
2. Quelles informations qualitatives peut-on tirer de l'observation des lignes de champ magnétiques quant à la nature de $Br$ à l'intérieur de la bobine ? 

II. Étude de l'influence du courant circulant dans la bobine

La sonde du teslamètre est placée au centre de la bobine. 
 
On fait varier l'intensité $I$ du courant dans la bobine et, pour chaque valeur de $I$, on note la valeur de $Br$
 
Le tableau ci-dessous comporte les valeurs de $I$ et $B$ obtenues : 
$$\begin{array}{|c|c|c|c|c|c|c|} \hline I(A)&0&1.5&2.5&3.5&4.5&5.0\\ \hline B(10^{-5}T&0&94&153&215&280&310\\ \hline \end{array}$$
 
1. Faire un schéma clair et annoté du montage à réaliser pour obtenir, faire varier, et mesurer l'intensité du courant $I$ dans le circuit de la bobine. 
 
2.1 Déterminer, à partir des données du tableau, la relation littérale entre $B$ et $I.$
 
2.2 Exprimer numériquement cette relation. 
 
3.1 Donner la relation théorique entre le champ $B$ et l'intensité $I.$
 
3.2 En déduire la valeur expérimentale de la perméabilité magnétique du vide $\mu_{0}$
 
3.3 Calculer l'erreur relative avec la valeur théorique. 

III. Étude de la valeur du champ magnétique le long de l'axe de la bobine

On maintient $I=4\,A$ dans la bobine. 
 
On mesure B en divers points le long de l'axe et à la distance $x$ du centre de la bobine. 
 
Le tableau ci-dessous donne les valeurs de $B$ en fonction de $x$ : 
$$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline x(cm)&0&4&8&12&14&16&18&20\\ \hline B(mT)&2.45&2.44&2.42&3.70&2.33&2.28&2.08&1.45\\ \hline \end{array}$$
 
1. Tracer la courbe représentant $B$ en fonction de $x.$ 
 
Commenter l'allure de la courbe. 
 
2. La courbe obtenue confirme-t-elle les informations obtenues à partir de l'observation des lignes de champ ? 
 
Justifier. 
 
3. Pour quelles valeurs de $x$ peut-on conclure que $B$ est constant à $5\%$ sur l'axe de la bobine ? 
 
Données : 
 
perméabilité magnétique du vide : $\mu_{0}=4\pi\cdot10^{-7}SI.$

Exercice 11

Mesure du champ magnétique terrestre
 
On souhaite mesurer la valeur du champ magnétique terrestre $B_{H}$, dont la valeur théorique dans le lieu de l'expérience est $B_{H}=2.0\cdot10^{-5}T.$
 
Pour cela, on dispose d'un solénoïde infiniment long de longueur $l=0.5\,m$, de section $S=80\,cm^{2}$, et comportant  $N=50$ spires. 
 
Les spires de ce solénoïde ne sont pas jointives, ce qui permet de voir   l'intérieur du solénoïde. 
 
On place en son centre une aiguille aimantée de façon à ce qu'elle soit perpendiculaire à la direction du champ magnétique $B_{S}$ créé par le solénoïde. 
 
Lorsque le solénoïde est parcouru par un courant d'intensité $I$, l'aiguille s'écarte de sa position initiale d'un angle $\alpha.$ 
 
Les angles obtenus pour différentes intensités sont rassemblés dans le tableau ci-dessous :
$$\begin{array}{|c|c|c|c|c|c|} \hline I(A)&0.1&0.2&0.3&0.4&0.5\\ \hline \alpha(\text{ en }^{\circ})&33&51&63&69&73\\ \hline \end{array}$$ 

I. Étude préalable du protocole expérimental

1. Rappeler les propriétés du champ magnétique à l'intérieur du solénoïde. 
 
Donner ses caractéristiques. 
 
2.1 De quels instruments de mesure a-t-on besoin pour faire les mesures ci-dessus ? 
 
2.2 Pourquoi a-t-on besoin de voir l'intérieur du solénoïde ? 
 
3. Selon quelle direction (Est-Ouest ou Nord-Sud) doit être disposé le solénoïde ? 
 
Justifier. 
 
4.1 Calculer le champ magnétique créé par le solénoïde en son centre, si celui-ci est parcouru par une intensité $I=10\,A.$
 
4.2 Pour quelle raison ne peut-on pas utiliser de telles intensités pour faire les mesures d'angles ? 
 
Combien vaudrait alors l'angle  

II. Exploitation des résultats

1.1 Faire un schéma « vu de dessus » de l'aiguille au centre du solénoïde lorsqu'elle est inclinée d'un angle $\alpha.$
 
Dessiner les vecteurs du champ magnétique terrestre $B_{H}$ et du champ magnétique créé par le solénoïde $B_{S}$
$$\alpha=arctan\left(\dfrac{\mu_{0}n\,I}{l\,B_{H}}\right)$$
 
1.2 Démontrer soigneusement que l'angle $\alpha$ est donné par l'expression : 
 
2.1 Tracer le graphique donnant la tangente de l'angle $\alpha$ $(\tan\alpha)$ en fonction de l'intensité $I.$
 
2.2 Calculer le coefficient directeur de la droite obtenue. 
 
2.3 En déduire la valeur du champ magnétique terrestre $B_{H}$
 
2.4 Calculer l'erreur absolue et l'erreur relative de votre mesure avec la valeur théorique.
 
Donnée : 
 
$\mu_{0}=4\pi\cdot10^{-7}SI.$

Exercice 12

On donne : 
 
$B_{H}=2\cdot10^{-5}T$ On prendra $4\pi=12.5$
 
1) Un solénoïde $S$, de centre $O$ et de longueur $L=62.5\,cm$, comportant $N=100$ spires, est parcouru par un courant électrique d'intensité constante $I=0.2\,A.$
 
a) Déterminer les caractéristiques du vecteur champ magnétique créé par le courant au point $O$ centre du solénoïde $S$
 
b) Sur la figure 2 (page 3 à compléter et à remettre avec la copie), 
 
Représenter le spectre magnétique créé par le courant à l'intérieur du solénoïde S et indiquer les faces de la bobine.
 
2) On place au point $O$ une petite aiguille aimantée mobile autour d'un axe vertical. 
 
Le solénoïde est placé de telle manière que son axe soit perpendiculaire au méridien magnétique.
 
a) Représenter sur la figure 3 (page 3 à compléter et à remettre avec la copie), les vecteurs $\overrightarrow{B}_{H}$ composante horizontale du vecteur champ magnétique terrestre et $\overrightarrow{B}_{C}$ le vecteur champ magnétique créé par le courant $I$ à l'intérieur du solénoïde en utilisant l'échelle : $1cm\ \rightarrow\ 10^{-5}T$, ainsi que la nouvelle position de l'aiguille aimantée.
 
b) Déterminer l'angle $\alpha$ que fait l'aiguille aimantée avec l'axe du solénoïde lorsque celle-ci prend une position d'équilibre stable.
 
3) On superpose avec les champs $\overrightarrow{B}_{C}$ et $\overrightarrow{B}_{H}$ un champ magnétique $\overrightarrow{B}_{a}$ créé par un aimant droit dont l'axe passe par $O$ et fait un angle $\theta=60^{\circ}$ avec l'axe du solénoïde. 
 
Le pôle nord de l'aimant se trouve à proximité du solénoïde (figure 4, page 3 à compléter et à remettre avec la copie). 
 
L'axe de l'aiguille aimantée s'oriente alors suivant une direction faisant un angle $\beta=45^{\circ}$ avec $\overrightarrow{B}_{H}.$ 
 
Montrer que la valeur du champ magnétique créé par l'aimant s'écrit sous la forme : 
$$B_{a}=\dfrac{B_{C}-B_{H}}{\sin\theta-\cos\theta}$$
 
Calculer sa valeur
 

 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Série d'exercices : Gravitation universelle - Ts

Classe: 
Terminale
 

Exercice 1

Un satellite artificiel de la Terre, de masse $m$, se déplace vitesse constante sur une orbite circulaire dans un référentiel galiléen lié au centre de la Terre à l'altitude $h=3.6\cdot10^{7}m$ compté à partir de la surface de la Terre. 
 
La trajectoire est située dans le plan équatorial et le satellite tourne dans le sens de rotation de la Terre.
 
Le rayon de la Terre est $R=6.4\cdot10^{6}m$
 
1. Calculer la valeur de l'intensité $g$ du champ de pesanteur à l'altitude $h$, sachant qu'à la surface de la Terre $g_{0}=9.8\,m\cdot s^{-2}.$ 
 
On rappelle la loi de la gravitation universelle $F=k\dfrac{Mm}{r^{2}}$0 où $M$ est la masse de la Terre et $r$ la distance du satellite au centre de la Terre.
 
2. Faire le bilan des forces appliquées au satellite supposé ponctuel et en déduire sa vitesse
 
3. Déterminer la période du mouvement dans le repère galiléen considéré ici.
 
 

Exercice 2

La Terre est assimilée à une sphère de rayon $T_{R}$ et de masse $M_{T}.$
 
Elle possède une répartition de masse à symétrie sphérique.
 
1. On suppose galiléen, le repère géocentrique dont l'origine coincide avec le centre de la Terre et dont les axes ont une direction fixe par rapport aux étoiles
 
Deux corps sphériques de masse $m_{1}$ et $m_{2}$, dont les centres sont distants de $r$ exercent l'un sur l'autre des forces d'attraction ayant pour intensité : $$F=G\dfrac{m_{1}m_{2}}{r^{2}}$$
 
$G$ est la constante de gravitation univerelle
 
1.1
 
1.1.1 Écrire l'expression de l'intensité $F_{0}$ de la force que la Terre exerce sur un corps ponctuel de masse $m=1Kg$ placé à surface
 
1.1.2 a) Déduire de la question 1.1.1, l'expression de la masse $M_{T}$ de la Terre en fonction de $g_{0}$, $R_{T}$ et $G$
 
b) Calculer $M_{T}$
 
On donne : 
 
$G=6.67\cdot10^{-11}S.I$, 
 
$g_{0}=9.8\,m\cdot s^{-2}$, 
 
$R_{T}=6370Km$
 
1.2 Montrer qu'a l'altitude $h$ au-dessus de la Terre, l'intensité du champ de gravitation est donnée par la relation : $$g=g_{0}\dfrac{R_{T}^{2}}{\left(R_{T}+h\right)^{2}}$$
 
$g_{0}$ est l'intensité du champ de gravitation terrestre au niveau du sol
 
2. Un satellite assimilé à un point matériel décrit une orbite circulaire dont son centre est confondu avec celui de la Terre.
 
Il est à l'altitude $h.$
 
2.1 Montrer que le mouvement du satellite est uniforme.
 
2.2 Établir en fonction $g_{0}$, $R_{T}$ et $h.$
 
2.2.1 la vitesse $v$ du satellite ;
 
2.2.2 La période $T$ du satellite ;
 
2.3 Calculer $v$ et $T$
 
2.4 On pose $r=R_{T}+h$
 
2.4.1 Montrer que le rapport $\dfrac{T^{2}}{r^{3}}=cte$ est égal à un constante.
 
C'est la $3^{e}$ de Kepler
 
2.4.2 Exprimer le rapport $\dfrac{T^{2}}{r^{3}}=cte$ en fonction de $M_{T}$ et $G$
 
2.4.3 Calculer la masse $M_{T}$ de la Terre.
 
Cette valeur est-elle compatible avec celle de la question 1.1.2 
 
On donne $h=300Km.$

Exercice 3

La terre est assimilée à une sphère homogène de centre $O$ de masse $M$ et de rayon $R.$ 
 
Le champ de gravitation crée par la Terre en tout point $A$ de l'espace situé à une distance $r$ du point $O$ est :
$$\overrightarrow{\mathfrak{G}}=-\dfrac{GM}{r^{2}}\overrightarrow{u}\quad\text{et}\quad\overrightarrow{u}=\dfrac{\overrightarrow{OA}}{\|\overrightarrow{OA}\|}$$
 
$G$ : Constante universelle de gravitation
 
1. Un satellite $(S)$ de masse $m$ décrit un mouvement uniforme sur une orbite circulaire de $r$ autour de la Terre.
 
Le mouvement est rapporté par rapport au repère géocentrique et on suppose que $(S)$ soumis à la seule action du champ de gravitation terrestre
 
1.1 Exprimer la vitesse $V$ de $(S)$ en fonction de l'intensité $G_{0}$ du champ de gravitation du sol, de $R$ et $r$
 
1.2 En déduire l'expression de la période $T$ du mouvement. 
 
Calculer $T$
 
On donne $R=6400Km$ ; 
 
$G_{0}=9.8\,m\cdot s^{-2}$ ; 
 
$r=8000Km$
 
2.
 
2.1 A partir du travail élémentaire $\mathrm{d}w=-f\mathrm{d}r$ de la force de gravitation exercée par la Terre sur le satellite ; montrer que le travail de cette force lors du déplacement du sol jusqu'à l'orbite de rayon $r$ est donné par : $$W=mG_{0}R^{2}\left(\dfrac{1}{r}-\dfrac{1}{R}\right)$$
 
2.2 En déduire l'expression de l'énergie potentielle du système Terre-satellite en fonction de $G_{0}$, $m$, $r$ et $R.$
 
On choisira le niveau du sol comme étant de référence pour l'énergie potentielle
 
2.3 Exprimer l'énergie cinétique de $(S)$ en fonction de $G_{0}$, $m$, $r$ et $R$
 
En déduire l'expression de l'énergie mécanique $E$
 
3. Il se produit une très faible variation $\mathrm{d}r$ du rayon $r$, telle que la trajectoire puisse toujours être considéré comme circulaire
 
3.1 Exprimer la variation $\mathrm{d}v$ de la vitesse qui en résulte et montrer que $\mathrm{d}v=-\dfrac{\pi}{T}\mathrm{d}r$ 
 
3.2 La variation de $\mathrm{d}r$ est en réalité due au travail $\mathrm{d}w_{f}$ des forces de frottements exercées par les couches raréfiées de l'atmosphère pendant le déplacement. 
 
Du signe de $\mathrm{d}w_{f}$, déduire l'effet de ces forces sur l'altitude et la vitesse de $(S).$

Exercice 4

On assimile le Soleil à une sphère de rayon $R_{S}$ et de masse $M_{S}$ présentant une répartition de masse à symétrie sphérique. 
 
On suppose que la trajectoire de la Terre autour du Soleil est un cercle de rayon $r.$
 
1. Donner l'expression littérale du champ de gravitation $G_{0S}$ à la surface du Soleil. 
 
Calculer sa valeur numérique.
 
2. Donner l'expression littérale du champ de gravitation $G_{S}$ en un point de l'orbite terrestre autour du Soleil. 
 
Calculer sa valeur numérique.
 
3. Comparer la valeur du champ de gravitation $G_{S}$ précédente à celle $G_{0}T$ du champ de gravitation terrestre au niveau du sol. 
 
Conclure.
 
Données :
 
$R_{S}=7.0\cdot10^{5}km$ 
 
$M_{S}=2.0\cdot10^{30}kg$ 
 
$r=1.5\cdot10^{8}km$
 
Constante de gravitation universelle : $G=6.67\cdot10^{-11}S.I.$
 
Champ de gravitation au niveau du sol : $G_{0}T=9.8\,N\cdot kg^{-1}$
 
Soit $M_{L}$ et $M_{T}$ les masses respectives de la Lune et de la Terre, ces astres étant supposés sphériques. 
 
Soit $R_{L}$ et $R_{T}$ leurs rayons. 
 
On a les relations $M_{T}=81\cdot M_{L}$ et $R_{T}=\dfrac{11}{3}R_{L}.$
 
4. Calculer la valeur du champ de gravitation lunaire $G_{0}L$ au niveau de son sol.
 
5. Il existe sur la ligne joignant les deux astres Terre et Lune un point où les champs de gravitation lunaire et terrestre se compensent.
 
a) Situer ce point $M$ remarquable en calculant sa distance $d$ au centre de la Terre.
 
b) Indiquer, sur le segment Terre-Lune, le domaine où l'action gravitationnelle d'un des deux astres est prépondérante.
 
Données : 
 
Distance Terre-Lune : $D=380\ 000\,km.$

Exercice 5

Données : 
 
Masse de la Terre $M_{T}=5.97\times 10^{24}kg$
 
Rayon de la Terre $R_{T}=6.38\times 10^{6}m$
 
Masse du Soleil $M_{S}=333\times 10^{3}\times M_{T}$
 
Constante universelle de gravitation $G=6.67\times 10^{-11}S.I.$
 
Valeur du champ de pesanteur au niveau du sol $g=9.81\,m/s^{2}$

1 Lancement d'un satellite

On étudie le lancement d'un satellite artificiel à partir d'un point $O$ de la surface terrestre.
 
1.a) Établir l'expression de la vitesse du point $O$ de la surface terrestre. 
 
Dans le référentiel géocentrique $R_{g}$ (assimilé ici à un référentiel galiléen) en fonction de la vitesse angulaire de rotation de la Terre autour de l'axe de ses pôles $($cette vitesse angulaire est notée $\Omega)$, du rayon terrestre $R_{T}$ et de la latitude $\lambda$ du lieu du lancement.
 
1.b) En déduire les conditions les plus favorables pour le lancement du satellite. 
 
Parmi les trois champs de tirs suivants, lequel choisir de préférence ?
 
Baïkonour au Kazakhstan $\lambda=46^{\circ}$ ;
 
Cap Canaveral aux USA $\lambda=28.5^{\circ}$ ;
 
Kourou en Guyane française $\lambda=5.23^{\circ}.$
 
1.c) Établir l'expression de l'énergie potentielle de gravitation d'un satellite en fonction de son altitude $z$ par rapport au sol. 
 
On prend pour référence une énergie potentielle nulle à l'infini. 
 
En déduire l'expression de l'énergie mécanique du satellite sur sa base de lancement dans le référentiel géocentrique.
 
1.d) On appelle ici vitesse de libération $v_{1}$, la vitesse verticale minimale qu'il faut communiquer initialement au satellite par rapport au sol, pour qu'il puisse se libérer de l'attraction terrestre. 
 
Donner l'expression de $v_{1}.$ 
 
Calculer sa valeur numérique dans le cas où le satellite est lancé de la base de Kourou (on tient donc compte de la rotation de la terre).

2. Satellite artificiel en orbite

On considère un satellite artificiel de masse $m$ en mouvement circulaire autour de la Terre.
 
2.a) Montrer que le mouvement du satellite est uniforme. 
 
Établir l'expression de la vitesse du satellite en fonction de son altitude ainsi que la troisième loi de Kepler liant la période de rotation $T$ du satellite au rayon $r$ de sa trajectoire.
 
2.b) Calculer le rayon de l'orbite d'un satellite géostationnaire .
 
2.c) Soit un satellite d'énergie mécanique initiale $Em_{0}.$ 
 
Son orbite est relativement basse et il subit donc les frottements des couches hautes de l'atmosphère. 
 
Il s'ensuit que l'énergie mécanique du satellite varie selon la loi :
 
$Em=Em_{0}(1+bt)$, $b$ étant un coefficient constant positif.
 
En supposant que la trajectoire reste approximativement circulaire.
 
Établir l'expression du rayon $r$ et de la vitesse $v$ du satellite en fonction du temps. 
 
Comparer les évolutions de $r$ et de $v$ ainsi que celles des énergies potentielle et cinétique. 
 
Que devient l'énergie perdue ?

Exercice 6

Pour mettre un satellite en orbite, une fusée $a$, au décollage, une poussée de $7.5\cdot10^{5}N.$ 
 
La masse totale de la fusée est de $40$ tonnes.
 
1. Quelle est l'accélération de la fusée ?
 
2. Le satellite est placé sur une orbite circulaire de rayon $r.$ 
 
Exprimer la vitesse $v$ et la période $T$ du mouvement du satellite en fonction de $K$, constante universelle de gravitation, $r$ et $M$, la masse de la terre. 
 
En déduire que $\dfrac{T^{2}}{R^{3}}=\text{constante}.$
 
3. La courbe reproduite en annexe donne la représentation graphique de $T^{2}$ en fonction de $r^{3}.$
 
Elle est obtenue à partir de données numériques sur la période $T$ et le rayon $r$ de quelques satellites qui tournent autour de la Terre. 
 
Déduire de la courbe la valeur de la masse $M$ de la Terre.
 
$K=6.67\cdot10^{-11}U.S.I.$
 
4. Le satellite est placé sur une orbite de rayon $r$, contenu dans le plan équatorial.
 
a) Exprimer les énergies potentielles $E_{P}$, $E_{C}$ et totale $E_{T}$ du satellite en fonction de la masse $M$ de la Terre, de la masse $m$ du satellite et de $r.$ 
 
$« E_{P}$ est nulle lorsque le satellite est infiniment éloigné de la Terre $».$
 
b) Avant d'être placé sur son orbite de rayon $r$, le satellite, était posé sur le sol, en un point $P$ de latitude $\gamma.$ 
 
Sa vitesse était, la vitesse $V_{e}$ due à la rotation de la Terre, supposée sphérique de rayon $R.$ 
 
Donner l'expression de $V_{e}$ en fonction de $ω_{T}$, vitesse angulaire de rotation de la Terre, $R$ et $\gamma.$ 
 
Déterminer les expressions des énergies potentielles $E_{P1}$, cinétique $E_{C1}$ et totale $E_{T1}$ du satellite au point $P.$
 
5. a) Pour placer le satellite sur son orbite, il a fallu lui fournir l'énergie $\Delta E=E_{T}-E_{T1}.$
 
Montrer que $\Delta E$ varie avec $\gamma.$
 
b) On considérera que le satellite tourne dans le même sens que la Terre. 
 
Où doit-on choisir les bases de lancement pour l'énergie $\Delta E$ soit minimale ?
 
6. La première vitesse cosmique $V_{1}$ est la vitesse de satellisation circulaire à basse altitude autour de la Terre d'un engin spatial. 
 
Calculer $V_{1}$ à l'altitude $h=100\,km.$
 
On donne $R=6400\,km$ et la masse $M$ de la Terre.
 
 

Exercice 7

Un satellite supposé ponctuel, de masse $m_{S}$, décrit une orbite circulaire d'altitude $h$ autour de la Terre assimilée à une sphère de rayon $R_{T}.$ 
 
On fera l'étude dans un référentiel géocentrique considéré comme galiléen.
 
1. Établir l'expression de l'intensité $g$ du vecteur champ de pesanteur à l'altitude $h$ en fonction de sa valeur $g_{0}$, au niveau du sol, de $R_{T}$ et de $h.$
 
2. Déterminer l'expression de la vitesse $v_{S}$ du satellite, celle de sa période et de son énergie cinétique.
 
Application numérique : 
 
$m_{S}=1020\,kg$ ; 
 
$g_{0}=9.81\,m/s^{2}$ ; 
 
$R_{T}=6400\,Km$ ; 
 
$h=400\,km.$
 
3. L'énergie potentielle du satellite dans le champ de pesanteur à l'altitude $h$ est donnée par la relation : 
$$E_{P}=-\dfrac{Km_{S}M_{T}}{R_{T}+h}$$ avec $K$, constante de gravitation et $M_{T}$ masse de la Terre et en convenant que $E_{P}=0$ pour $h_{P\infty}.$
 
Justifier le signe négatif et exprimer $E_{P}$ en fonction de $m_{S}$, $g_{0}$, $R_{T}$ et $h.$ 
 
Déterminer l'expression de l'énergie mécanique $E$ du satellite puis comparer $E_{P}$ à $E_{C}$ et $E$ à $E_{C}.$
 
4. On fournit au satellite un supplément d'énergie $\Delta E=+5\cdot10^{8}J.$
 
Il prend alors une nouvelle orbite circulaire. 
 
Déterminer :
 
a) Sa nouvelle énergie cinétique et sa vitesse
 
b) Sa nouvelle énergie potentielle et son altitude.

Exercice 8

Le $15$ octobre $1997$, le véhicule spatial Cassini emportait à son bord la sonde HUYGENS destinée à l'exploration des anneaux de Saturne.
 
Titan, le plus gros satellite de Saturne, a été découvrent en $1665$
 
On étudie le mouvement supposé circulaire de Titan dans le référentiel centré sur Saturne et dont les trois axes sont dirigés vers trois étoiles lointaines supposées fixes
 
1. Reproduire le schéma ci-dessus et représenter qualitativement la force gravitationnelle qui agit sur Titan
 
2. Donner l'expression vectorielle de cette force
 
3. Établir du vecteur accélération du centre d'inertie de Titan sur son orbite et le représenter qualitativement sur le schéma précédent
 
4. Montrer que le mouvement de Titan sur son orbite est uniforme
 
5. Établir en fonction de $G$ $M_{S}$ et $r_{T}$ :
 
5.1 l'expression de la vitesse $V_{T}$ du centre d'inertie de Titan
 
5.2 l'expression de la période de révolution $T_{T}$ de Titan autour de Saturne
 
6. Montrer qu'au cours de sa révolution autour de Saturne :
 
$\dfrac{T_{T}^{2}}{r_{T}^{3}}=K=\text{constante}$ $(3^{e}$ loi de Kepler$)$
 
7. En fait Saturne possède un cortège de satellites dont au moins $60$ ont été identifiés à ce jour.
 
Parmi eux, figurent Rhéa et Dioné découverts par Jean Dominique Cassini respectivement en $1672$ et $1684$
 
7.1 Montrer que ces deux satellites vérifient la $3^{e}$ loi de Kepler
 
7.2 En déduire la masse $M_{S}$ de Saturne
 
On donne :
 
$-\ $ Constante de gravitation universelle $G$ : $G=6.67\cdot10^{-11}S.I$
 
$-\ $ Rayon de l'orbite de Rhéa $r_{R}=527070\,Km$
 
$-\ $ Période de révolution de Rhéa autour de Saturne $T_{R}=4.518\,jours$ soit $390355\,s$
 
$-\ $ Rayon de l'orbite de Dioné $r_{D}=377400\,Km$
 
$-\ $ Période de révolution de Dioné autour de Saturne $T_{D}=2.737\;jours$ soit $236477\,s$
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 
Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Série d'exercices : Dynamique - Ts

Classe: 
Terminale
 

Exercice 1

Dans ce problème on prendra $g=10\,m\cdot s^{-2}.$ 
 
Tous les calculs seront effectués à $10^{-2}$ près.
 
Un solide $(S)$ de masse $m=50\,g$, de dimension négligeable, peut glisser sur une piste $ABCD$ située dans un plan vertical :
 
$-\ $ $AB$ est la ligne de plus grande pente d'un plan incliné d'un angle $\alpha=30^{\circ}$ par rapport à l'horizontale ; $AB=1.6\,m.$
 
$-\ $ $BCD$ est le quart d'un cercle de centre $I$ et de rayon $r=0.9\,m$ ; $C$ est situé sur la verticale passant par $I$ (voir figure).
 
1) On néglige les frottements. 
 
Le solide $(S)$ part du point $A$ sans vitesse.
 
a) Calculer sa vitesse en $B$, en $C$ et en $D.$
 
b) Calculer l'intensité de la force $\overrightarrow{R}$ exercée par la piste sur le solide $(S)$ en $C$ et en $D.$
 
c) Donner les caractéristiques du vecteur vitesse $\overrightarrow{V_{D}}$ du solide $(S)$ au point $D.$
 
2) On néglige la résistance de l'air. 
 
A partir du point $D$, le solide $(S)$ tombe dans le vide avec la vitesse $\overrightarrow{V_{D}}$ précédente. 
 
Le point $C$ est situé à la hauteur $h=1.55\,m$ du sol horizontal.
 
a) Donner l'équation cartésienne de la trajectoire du mouvement de $(S)$ à partir du point $D$, dans le repère $(O\;,\ x\;,\ z).$
 
b) Jusqu'à quelle hauteur $H$ au-dessus du sol horizontal monte le solide $(S)$ ?
 
c) Calculer la distance $OP$ où $P$ est le point d'impact du solide $(S)$ sur le sol horizontal.
 
3) Dans cette question, la piste exerce au mouvement du solide $(S)$ une force de frottements $\overrightarrow{f}$ parallèle et de sens contraire à sa vitesse à chaque instant, et d'intensité constante le long de $ABCD.$ 
 
Partant de $A$ sans vitesse, le solide $(S)$ s'arrête au point $D.$
 
a) Établir en fonction de $m$, $g$, $R$ et $\alpha$, l'expression algébrique du travail $W_{\overrightarrow{f}}$ de la force de frottements entre les points $A$ et $D.$ 
 
Calculer $W_{\overrightarrow{f}}$
 
b) En déduire l'intensité de la force $\overrightarrow{f}$
 
On donne : $\cos 30^{\circ}=0.86.$
 
 

Exercice 2

Un avion de guerre supersonique est animé d'un mouvement rectiligne uniforme à la vitesse $V_{0}=400\,m\cdot s^{-1}$ vole à une altitude de $2000\,m$, son radar a détecté un véhicule de transport de soldats ennemis supposé ponctuel, immobile au point $A$, le pilote a décidé de les attaquer, malgré l'interdiction de ce fait par la loi de Genève. 
 
 
En passant par $O$ origine du repère l'avion $(O\;,\ \vec{i}\;,\ \vec{j})$, a lâché, à une date prise comme origine de temps, une bombe qui après quelques secondes adétériorécomplètement le véhicule et a tué tous les soldats.
 
En négligeant la force résistance de l'air et en appliquant la relation fondamentale de la dynamique à la bombe déterminer les composantes selon l'axe $(0\;,\ x)$ et selon l'axe $(O\;,\ y)$ de son accélération.
 
1) Établir les lois horaires de mouvement de la bombe selon les deux axes.
 
2) En déduire l'équation de la trajectoire de la bombe relativement au repère $(O\;,\ \vec{i}\;,\ \vec{j}).$
 
3) A quelle distance de la verticale passant par $O$ se trouvait le véhicule ? 
 
Déterminer la date d'arrivée de la bombe au véhicule.
 
4) Où se trouvait l'avion à la date d'arrivée de la bombe au véhicule ?
 
Déterminer les caractéristiques du vecteur vitesse de la bombe lorsqu'elle se trouvait à $1000\,m$ au-dessus du sol.

Exercice 3

Dans tout le problème, on néglige les frottements et on prend pour l'intensité de pesanteur $g=10\,m\cdot s^{-2}.$
 
Un pendule simple est constitué par une bille ponctuelle $M_{1}$ de masse $m_{1}=200\,g$ suspendue au bout d'un fil inextensible de masse négligeable et de longueur $\ell=0.9\,m.$
 
1) On écarte le pendule d'un angle $\alpha$ par rapport à sa position d'équilibre verticale et on le lâche sans vitesse initiale. 
 
La vitesse de la bille $M_{1}$ lors de son passage à la position
d'équilibre est $v=3\,m\cdot s^{-1}.$ 
 
Calculer la valeur de l'angle $\alpha.$
 
2) Lors de son passage à la position d'équilibre la bille $M_{1}$ heurte, au cours d'un choc parfaitement élastique, une autre bille ponctuelle $M_{2}$ immobile de masse $m_{2}=100\,g.$ (figure)
 
2) La vitesse de la bille $M_{2}$, juste après le choc, est $v_{A}=4\,m\cdot s^{-1}.$ 
 
Calculer la vitesse de la bille $M_{1}$ juste après le choc en appliquant la conservation de la quantité de mouvement.
 
3) La bille $M_{2}$ est propulsée avec la vitesse $V_{A}$ sur une piste qui comporte trois parties :
 
$-\ $ Une partie horizontale $AB$,
 
$-\ $ Une certaine courbe $BC$,
 
$-\ $ Un arc de cercle $CD$, de rayon $r$ et de centre $O.$
 
Les points $O$, $A$, $B$ et $E$ se trouvent dans un même plan horizontal.
 
a) Exprimer, en fonction de $g$, $r$, $\beta$ et $v_{A}$, la vitesse de la bille $M_{2}$ au point $I$
 
b) Exprimer, en fonction de $m_{2}$, $g$, $r$, $\beta$ et $v_{A}$, l'intensité de la réaction de la piste sur la bille $M_{2}$ au point $I.$
 
c) La bille $M_{2}$ arrive au point $D$ avec une vitesse horizontale de valeur $v_{D}=1\,m\cdot s^{-1}.$ 
 
Calculer la valeur de $r.$
 
4) Arrivée au point $D$, la bille $M_{2}$ quitte la piste avec la vitesse $\overrightarrow{V_{D}}$  précédente et tombe en chute libre.
 
a) Établir l'équation cartésienne de la trajectoire de la bille $M_{2}$ dans le repère $(O\;,\ \vec{i}\;,\ \vec{j}).$
 
b) Calculer la distance $OE.$
 
 

Exercice 4

Dans tout l'exercice, on suppose que le mouvement des protons a lieu dans le vide. 
 
Et on néglige leur poids devant les autres forces. 
 
On considère le dispositif de la figure ci-dessous.
 
Des protons sont émis en $C$ avec une vitesse quasiment nulle, puis accélérés entre les points $C$ et $D$ des plaques $P_{1}$ et $P_{2}$
 
1. Préciser le signe de la tension $U_{CD}$ pour que les électrons soient accélérés. 
 
Justifier votre réponse.
 
2. On posera par la suite $|U_{CD}|=U$
 
2.1 Exprimer la vitesse d'un proton en $D$ en fonction de $U$, $e$ et $m_{p}$
 
2.2 Calculer cette vitesse.
 
3. Après la traversée de la plaque $P_{1}$ en $D$, les électrons pénètrent en $O$ entre deux plaques parallèles $P_{3}$ et $P_{4}$ de longueur $l$ et distantes de $d.$ 
 
La tension $U'$ appliquée entre ces plaques crée un champ électrostatique $\overrightarrow{E}$ uniforme.
 
On donne $l=20\,cm$ et $d=7\,cm.$
 
3.1 Montrer que l'énergie cinétique se conserve entre $D$ et $O.$
 
3.2 Établir dans le repère $(O\;,\ \vec{i}\;,\ \vec{j})$ les équations du mouvement d'un proton dans la région limitée par les deux plaques $P_{3}$ et $P_{4}$
 
3.3 Vérifier que l'équation de la trajectoire peut s'écrire :$$y=-\dfrac{U'}{4dU}x^{2}$$
 
3.4 Déterminer la condition à laquelle doit satisfaire la tension $U'$ pour que les protons sortent du champ électrostatique $\overrightarrow{E}$ sans heurter la plaque $P_{4}$
 
3.5 Déterminer $U'$ pour que les protons sortent du champ en passant le point $S$ de coordonnées $\left(l\;,\ -\dfrac{d}{5}\right)$
 
4. A la sortie du champ électrostatique par le point $S$, les protons sont reçus en $J$ sur un écran plat $E$ placé perpendiculairement à l'axe $Ox$
 
4.1 Représenter qualitativement la trajectoire d'un proton entre $O$ et $J$
 
4.2 Établir l'expression littérale de la déviation $O'J$ du spot sur l'écran
 
4.3 Calculer la distance $O'J.$
 
On donne : 
 
$L=20\,cm$ ; 
 
$U=10^{3}V$ ; 
 
masse du proton : $m_{p}=1.67\cdot10^{-27}kg$ ;
 
$OI=\dfrac{l}{2}$ 
 
Charge élémentaire : $e=1.6\cdot10^{-19}C$
 
 

Exercice 5

 
Un dispositif permet de lancer une bille à la vitesse $v_{0}=16\,m\cdot s^{-1}.$
 
La bille part d'un point $O$, vers le haut, suivant une direction faisant l'angle $\alpha$ avec la verticale.
 
1) Déterminer les lois horaires du mouvement.
 
2) Quelle est l'équation de la trajectoire ?
 
3) a) Pendant combien de temps la bille s'élève-t-elle avant de descendre ?
 
b) Quelle est sa vitesse à la fin de cette phase ascendante ? $(\alpha=50^{\circ})$
 
4) Quelle est l'altitude maximale atteinte par la bille, comptée à partir de son point de départ $O$ ?
 
La bille retombe sur l'axe $Ox$ en $P.$
 
5) a) Déterminer la distance $OP.$
 
b) Pour quelle valeur de $\alpha$, $OP$ est-elle maximale ?
 
Soit $Q$ un point de l'axe $Ox$ d'abscisse $x_{0}=10\,m.$
 
6) Montrer qu'il y a deux angles de tir $\alpha_{1}$ et $\alpha_{2}$ permettant d'atteindre $Q.$
$$\left(\dfrac{1}{\sin^{2}\alpha}=\dfrac{\sin^{2}\alpha+\cos^{2}\alpha}{\sin^{2}\alpha}=1+cot\,g^{2}\alpha\right)$$

Exercice 6

Une balle $B$ de mini-golf est poussée en $A$ à l'aide d'un club. 
 
La balle, supposée ponctuelle, dévale la pente $AC$ et décolle en $C$ où elle commence alors un mouvement aérien vers le trou noté $T.$
 
On se propose d'étudier le mouvement de la balle $B$ dans le repère $(O\;,\ x\;,\ z)$ supposé galiléen.
 
Dans tout l'exercice, on ne considèrera aucune force liée à l'atmosphère.
 
On précise que $z_{C}=40\,cm$ et $g=9.8\,N\cdot kg^{-1}.$
 
 
I. La trajectoire balistique de $C$ vers $T.$
 
La balle quitte le point $C$ de la rampe à la date $t=0s$ avec une vitesse $v_{0}$ horizontale égale à $2.0\,m\cdot s^{-1}.$
 
a) Qu'est-ce qu'un référentiel galiléen ?
 
b) Faire le bilan des forces qui s'exercent sur la balle lors de cette phase. 
 
Conclure.
 
c) Établir les équations horaires de la vitesse et de la position de la balle $B.$
 
d) En déduire l'équation $z(x)$ de la trajectoire de la balle $B.$
 
e) Quel doit être alors l'abscisse $x_{T}$ du trou $T$ pour que la balle tombe directement dedans ?
 
f) Déterminer la date $t_{F}$ à laquelle la balle $B$ tombe dans le trou.
 
II. Le mouvement sur la rampe
 
La balle quitte le point $A$ avec une vitesse de $0.80\,m\cdot s^{-1}.$
 
a) Déterminer la hauteur $z_{A}$ de $A$ nécessaire pour que la balle arrive en $C$ avec la vitesse de $2.0\,m\cdot s^{-1}.$
 
b) Expliquer pourquoi la vitesse $v_{0}$ est parfaitement horizontale lorsque la balle quitte le point $C.$

Exercice 7

Lors d'un match de basket, pour marquer un panier, il faut que le ballon passe dans un cercle métallique situé dans un plan horizontal, à $3\,m$ du sol. 
 
On assimile le ballon à un point matériel qui doit passer exactement au centre $C$ du cercle métallique. 
 
$xOy$ est un plan vertical contenant le point $C$ ; $xOz$ est le plan du sol supposé horizontal.
 
1) D'un point $A$ de $Oy$ situé à $2\,m$ du sol, un basketteur, sans adversaire, lance le ballon, avec une vitesse $\overrightarrow{V_{0}}$ contenue dans le plan
 
 
$xOy$ et dont la direction fait un angle $\alpha=45^{\circ}$ avec un plan horizontal.
 
On négligera l'action de l'air et on prendra $g=10\,m\cdot s^{-2}.$
 
a) Montrer que la trajectoire est plane.
 
b) Établir l'équation de cette trajectoire dans le système d'axes indiqué, en fonction de la valeur $V_{0}$ de la vitesse initiale.
 
c) Quelle doit être la valeur de $V_{0}$ pour que le panier soit réussi, sachant que les verticales de $A$ et de $C$ sont distantes de $7.1\,m$ ?
 
d) Quelle est la durée du trajet effectué par le ballon du point $A$ au point $C$ ?
 
2) Voulant arrêter le ballon, un adversaire situé à $0.9\,m$ du tireur, saute verticalement en levant les bras. 
 
La hauteur atteinte alors par ses mains est de $2.7\,m$ au-dessus du sol.
 
$\alpha$ et $V_{0}$ ayant les mêmes valeurs que précédemment, le panier sera-t-il marqué ?

Exercice 8

Les parties $(A)$ et $(B)$ sont indépendantes. 

On donne $g=10\,m\cdot s^{-2}.$
 
A. Dans cette partie les frottements sont supposés négligeables.
 
A l'origine des dates, un solide $S_{1}$ supposé ponctuel, de masse $m_{1}=200\,g$ est lâché sans vitesse initiale en un point $A$ d'un plan incliné (fig 1) dont la ligne de plus grande pente fait un angle $\alpha=30^{\circ}$ avec l'horizontale. 
 
 
Le solide $(S_{1})$ glisse sans frottement et arrive au point $B$, à la date $t_{B}$, ayant la vitesse $V_{B}.$
 
1) a) Représenter les forces exercées sur le solide $(S_{1})$
 
b) Établir l'expression de son accélération $a$, déduire la nature de son mouvement.
 
Calculer la valeur de $a.$
 
2) a) Calculer la valeur de la vitesse $V_{B}$ sachant que la distance $AB=2.5\,m.$
 
b) Calculer la durée $t_{B}$ du trajet $AB.$
 
B. Dans cette partie les frottements ne sont plus négligeables
 
Dans cette partie on relie le solide $(S_{1})$ à un solide $(S_{2})$ de masse $m_{2}=m_{1}$ par un fil inextensible, de masse négligeable, qui passe sur la gorge d'une poulie $(P)$ à axe fixe, dont on néglige la masse. 
 
A l'origine des dates $(t=0)$, $(S_{1})$ part de $B$ vers $A$ sans vitesse initiale. 
 
Au cours de son mouvement $(S_{1})$ est soumis à une force de frottement $\overrightarrow{f}$ supposée constante, parallèle à la ligne de plus grande pente du plan incliné et de sens opposé au mouvement. (fig 2)
 
 
1) a) En appliquant la deuxième loi de Newton $(R.F.D)$ au système, établir l'expression de son accélération $a$ et déduire la nature du mouvement.
 
b) Sachant que la valeur de $f$ est égale à $0.2\,N$, calculer $a.$
 
2) A l'instant de date $t_{C}=1\,s$, le solide $(S_{1})$ arrive en $C$ à la vitesse $V_{C}.$ 
 
Calculer $V_{C}.$
 
3) Au passage du solide $(S_{1})$ par le point $C$, le fil est coupé.
 
a) Donner l'expression de la nouvelle accélération $a_{1}$ du solide $(S_{1})$ après la coupure du fil, déduire la nature de son mouvement.
 
b) Calculer la distance maximale $($par rapport au point $C)$ parcourue par le solide $(S_{1})$ après la coupure du fil.
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 
Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Les acides a-aminés - Ts

Classe: 
Terminale
 

I. Généralités sur les acides $\alpha-$ aminés

1. Définition

On appelle acide aminé ou aminoacide, un composé organique renfermant, dans la même la molécule les deux groupements fonctionnels carboxyle et amino : c'est un composé  polyfonctionnel
 
L'acide est $\alpha–$ aminé si le groupement amino est fixé sur le carbone directement lié au carbone du groupement carboxyle
 
La formule générale sera 
 
Le groupe amino $-$ $NH_{2}$ est fixé sur le carbone situé en $\alpha$ du groupe carboxyle

2. Nomenclature

2.1 Nomenclature systématique

Le nom de l'acide $\alpha-$ aminé s'obtient en faisant précéder du terme $2-$ amino le nom de l'acide correspondant
 
En effet, pour un acide $\alpha-$ aminé ; c'est nécessairement le carbone numéro $2$ qui porte le groupe $-NH_{2}$ puis que le carbone du groupe carboxyle situé en bout de chaine porte le numéro $1$

Exemples :

$H_{2}N-CH_{2}-COOH$ : Acide amino éthanoïque 
 
 
 
 

2.2 Nomenclature usuelle

Les acides $\alpha-$ aminés naturels qui ont une très grande importance biologique ont des noms consacrés par l'usage

Exemples 

$H_{2}N-CH_{2}-COOH$ : Glycine (Gly)
 
 
 

II. La stéréochimie

1. Carbone asymétrique 
 
Un carbone asymétrique est un carbone tétragonal lié à quatre atomes ou groupements différents. 
 
On le repère habituellement par un astérisque $(\ast)$

Exemples

 

2. Chiralité

La chiralité est la propriété d'un objet de ne peut être superposable à son image dans un miroir

Remarques

$-\ $ Une molécule qui comporte un seul carbone asymétrique est toujours chirale
 
$-\ $ Une molécule comportant plusieurs carbones asymétriques peut être achirale
 
$-\ $ Une molécule ou un objet qui possède un centre de symétrie ou plan de symétrie n'est pas chirale

Remarque :

Les acides $\alpha-$ aminés naturels : sont tous chirals (et donc optiquement actifs), à l'exception de la glycine pour laquelle le substituant latéral est un atome d'hydrogène sont tous de configuration $“L”$ selon la convention de Fischer 

3. Énantiomérie

L'énantiomérie est la relation existant entre deux stéréoisomères de configurations image de l'une de l'autre dans un miroir et non superposables 

De manière générale :

Deux stéréoisomères non superposables et image de l'une de l'autre dans un miroir sont appelés énantiomères (ou énantiomorphes ou antipodes optiques)
 
La représentation de Cram permet de représenter la géométrie spatiale des molécules : les liaisons situées dans le plan sont représentées par un trait plein, les liaisons pointant vers l'avant par un triangle plein et celles pointant vers l'arrière par un triangle hachuré
 
 

4. Représentation de Fischer                                                                                                                                                    

La représentation de Fischer s'obtient en projetant la structure spatiale sur le plan en respectant impérativement les conventions suivantes :                                                                                                                          
 
$-\ $ la chaine carbonée est disposée dans le plan vertical 
 
$-\ $ le groupe  en haut, le groupe en bas
 
$-\ $ ces deux groupes vers l'arrière 
 
 
En projetant sur le plan de la feuille, on obtient deux  représentations possibles 
 
 
Dans la représentation (a), le groupe $-NH_{2}$ se situe à gauche de la chaine carbonée, par convention l'isomère a la configuration $L$ Dans la représentation (b), le groupe $-NH_{2}$ se projette à droite de la chaine carbonée, par convention l'isomère a la configuration $D$

III. Quelques propriétés des acides $\alpha-$ aminés

1. Activité optique

Ces substances ont la propriété de faire tourner le plan de la polarisation d'une lumière polarisée 
 
$-\ $ soit à droite : la substance est dite dextrogyre ou présente le pouvoir rotatoire $(+)$
 
$-\ $ soit à gauche : elle dite lévogyre ou présente  un pouvoir rotatoire $(-)$
 
Le mélange en proportion équimolaire de ses deux isomères $(+)$ et $(-)$ est sans sur la lumière polarisée.
 
Ce mélange est appelée mélange racémique ou inactif par compensation

Remarque :

Les lettres $D$ et $L$ représente la configuration du carbone asymétrique dans chacun des énantiomères et non le signe de leur pouvoir rotatoire

2. Propriétés acido-basiques des acides $\alpha-$ aminés

Les acides $\alpha-$ aminés possèdent à la fois les propriétés des acides carboxyliques et des amines.
 
Comme un acide avec une amine, le composé $R-CH\left(NH_{2}\right)-COOH$ ne peut pas exister en solution aqueuse. 
 
Il sous la forme : 
 
 
Cette espèce chimique est appelée zwitterion ou amphion ou ion dipolaire. 
 
Un acide carboxylique réagit avec une amine selon la réaction : 
 
$R_{1}-COOH+R_{2}-NH_{2}\ \longrightarrow\ R_{1}-COO^{-}+R_{2}-NH_{3}^{+}$
 
L'acide fournit un proton qui est capté par la base.
 
Dans le cas d'un acide $\alpha-$ aminé, cette réaction acide-base se produit de manière intramoléculaire
 
$H_{2}N-CHR-COOH\ \longrightarrow\ H_{3}N^{+}-CHR-COO^{-}$
base        acide                  zwittérion
 
On passe de la forme moléculaire à la forme zwittérion (amphion)
 
A l'état solide une molécule d'acide $\alpha-$ aminé se trouve sous la forme zwittérion  
 
En solution aqueuse, en l'absence d'apport d'acide et de base, la forme zwittérion est largement prépondérante

2.1 Forme cationique en milieu acide

En milieu fortement acide, les ions $H_{3}O^{+}$ réagissent avec le zwittérion selon la réaction pratiquement totale :
 
$H_{3}N^{+}-CHR-COO^{-}+H_{3}O^{+}\ \longrightarrow\ H_{3}N^{+}-CHR-COOH+H_{2}O$
 
On obtient la forme cationique
 
Le couple cation$/$zwittérion est : $H_{3}N^{+}-CHR-COOH|H_{3}N^{+}-CHR-COO^{-}.$
 
Il est caractérisé par un $pKa_{1}.$
 
L'espèce majoritaire à $pH<pKa_{1}$ est l'acide du couple, c'est-à-dire, la forme cationique

2.2 Forme anionique en milieu basique

En milieu fortement basique, les ions $OH^{-}$ majoritaire réagissent avec le zwittérion en déprotonant le groupe ammonium $–NH_{3}^{+}$ selon une  réaction pratiquement totale :
 
$H_{3}N^{+}-CHR-COO^{-}+OH^{-}\ \longrightarrow\ H_{2}N-CHR-COO^{-}+H_{2}O$
 
On obtient la forme anionique 
 
Le couple zwittérion$/$anion est : $H_{3}N^{+}-CHR-COO^{-}|H_{2}N-CHR-COO^{-}.$
 
Il est caractérisé par un $pKa_{2}.$
 
L'espèce majoritaire à $pH>pKa_{2}$ est l'acide du couple, c'est-à-dire, la forme anionique

2.3 Forme prédominante selon $pH$

 

2.4 Point isoélectrique

Pour chaque acide aminé, il existe une valeur spécifique du $pH$ où la charge globale de la molécule est nulle. 
 
Cette valeur de $pH$ (pHi) représente le point isoélectrique où la concentration du zwitterion de l'acide aminé est maximale.
 
La charge globale portée par les différentes formes ioniques de l'acide aminé en solution dépend de la valeur du $pH$ de la solution.
 
La charge électrique globale est nulle lorsque le $pH$ de la solution est égal au $pH_{i}.$
 
Le point isoélectrique peut être estimé à partir de l'équation de Henderson-Hasselbalch :
 
$pH=pKa_{1}+\log\dfrac{\left[R-CH\left(NH_{3}^{+}\right)-COOH\right]}{\left[R-CH\left(NH_{3}^{+}\right)-COO^{-}\right]}$ ;
 
$pH=pKa_{2}+\log\dfrac{\left[R-CH\left(NH_{3}\right)-COO^{-}\right]}{\left[R-CH\left(NH_{3}^{+}\right)-COO^{-}\right]}$ 
 
Au point isoélectrique $pH=pH_{i}$
 
et $\left[R-CH\left(NH_{3}^{+}\right)-COOH\right]=\left[R-CH\left(NH_{3}\right)-COO^{-}\right]$
 
$\Rightarrow 2pH_{i}=pKa_{1}+pKa_{2}+\log\dfrac{\left[R-CH\left(NH_{3}^{+}\right)-COOH\right]}{\left[R-CH\left(NH_{3}^{+}\right)-COO^{-}\right]}+\log\dfrac{\left[R-CH\left(NH_{3}\right)-COO^{-}\right]}{\left[R-CH\left(NH_{3}^{+}\right)-COO^{-}\right]}$ 
 
$\Rightarrow 2pH_{i}=pKa_{1}+pKa_{2}+\log\dfrac{\left[R-CH\left(NH_{3}^{+}\right)-COOH\right]}{\left[R-CH\left(NH_{3}^{+}\right)-COO^{-}\right]}\times\dfrac{\left[R-CH\left(NH_{3}\right)-COO^{-}\right]}{\left[R-CH\left(NH_{3}^{+}\right)-COO^{-}\right]}=pKa_{1}+pKa_{2}$ 
 
$\Rightarrow \boxed{pH_{i}=\dfrac{pKa_{1}+pKa_{2}}{2}}$
 
Elle est positive lorsque le pH de la solution est inférieur au $pH_{i}$ et négative lorsque le $pH$ de la solution est supérieur au $pH_{i}.$

IV. Les polypeptides et les protéines

1. Les polypeptides

1.1 Liaison peptidique 

Cette liaison s'établit entre la fonction amine d'un acide aminé et la fonction acide d'un autre acide aminé selon le schéma :
 
 
En fonction du nombre d'acides aminés liés les uns aux autres, on est en présences des peptides ou des polypeptides.
 
A partir de cinquante acides aminés environ, les composés sont appelés protéines
 
Lors qu'on écrit la formule d'un peptide, on écrit toujours à gauche le groupement $-NH_{2}$ terminal et à droite le groupement $–COOH$ terminal

Exemple :

Le tripeptide formé dans l'ordre par les trois acides $\alpha-$ aminés Gly, Ala, Val, s'écrit donc :
 
$H-$Gly$-$Ala$-$Val$-OH$

1.2 Synthèse des peptides

Si mélange plusieurs acides aminés, les possibilités  de combinaison augmentent avec le nombre d'acides aminés 
 
Pour obtenir un peptide donné, on bloque certaines fonctions et on active d'autres
 
Il faut que ces réactions soient réversibles. 

Par exemple :

$-\ $ on bloque la fonction carboxyle par la formation d'un ester 
 
$-\ $ on bloque la fonction amine par la formation d'un amide
 
$-\ $ on active la fonction carboxyle en la transformant en chlorure d'acyle
 
$-\ $ on débloque le groupe amino et le groupe carboxyle des acides$ -\alpha$ aminés qui étaient bloqués.

Exemple : 

synthèse du dipeptide $H-$Gly$-$Ala$-OH$
 
 

Remarque :

La dénomination d'acide $\alpha-$ aminé $N-$ terminal est réservée à celui qui porte la fonction amine $-NH_{2}$ libre et d'acide $\alpha-$ aminé $C-$ terminal à celui qui porte le groupe carboxyle libre $-COOH$

2. Les protéines

Les protéines sont des polypeptides complexes de masse molaire très élevée 
 
Ce sont des macromolécules formées par un enchainement d'acides $\alpha-$ aminés : ce sont des polyamides

Remarques :

$-\ $ La structure primaire d'une protéine est définie par la nature des acides 
 
$\alpha-$ aminés constitutifs et par l'ordre selon lequel ils sont assemblés dans la chaine du polypeptide
 
$-\ $ On obtient des acides $\alpha-$ aminés constitutifs par hydrolyse soit à chaud en milieu acide ; soit dans des conditions beaucoup plus douces en présence en d'enzymes

Exemple : 

Hydrolyse du tripeptide  Ala$-$Gly$-$Ala
 
$H_{2}N-CH\left(CH_{3}\right)-CO-NH-CH_{2}-CO-CH\left(CH_{3}\right)-COOH+2H_{2}O\ \longrightarrow\ H_{2}N-CH_{2}-COOH+2H_{2}N-CH\left(CH_{3}\right)-COOH$

Compléments 

Une protéine, aussi appelée protide (anglicisme) est un assemblage (ou séquence) d'acides aminés liés par des liaisons peptidiques. 
 
On parle de protéine lorsque plus de $50$ acides aminés sont liés au sein d'une chaîne d'acides aminés. 
 
Les propriétés des acides aminés (charge, hydrophobicité...) gouvernent la structure de la protéine, globulaire ou fibrillaire, que l'on peut décrire à différents niveaux :
 
$-\ $ la structure primaire, qui est la séquence linéaire des acides aminés dans la protéine ; 
 
$-\ $ la structure secondaire, qui rend compte de l'organisation de groupes d'acides aminés en éléments structuraux simples : hélices alpha, feuillets et tours béta, autres structures ; 
 
$-\ $ la structure tertiaire, qui correspond au repliement de la protéine dans l'espace tridimensionnel (on parle aussi de structure tridimensionnelle décrite par les coordonnées des atomes dans l'espace). 
 
Cette structure rend compte de l'organisation entre eux des éléments de structure secondaire ; 
 
$-\ $ la structure quaternaire, qui définit l'association (multimérisation) entre des protéines de structures primaires identiques (homoassociation) ou distinctes (hétéroassociation). 
 
Les protéines ont des fonctions très diverses : certaines pourront avoir une fonction structurale (elles participent à la cohésion structurale des cellules entre elles), enzymatique (elles catalysent les réactions chimiques de la matière vivante) ou encore une fonction de messager (pour les protéines impliquées dans des processus de signalisation cellulaire

Exercice d'application

Les protéines entrent dans la constituions  des organismes vivants et participent a leur fonctionnement en intervenant dans un grand nombre de réactions biochimique.
 
Ceux sont des macromolécules constitues par association d'acide $\alpha-$ aminé par liaison peptidique.
 
On donne les masses molaires :
 
$M_{C}=12g/mol$
 
$M_{H}=1g/mol$ 
 
$M_{N}=14g/mol$ 
 
$M_{O}=16g/mol$ 
 
$M_{Na}=23g/mol$
 
On se propose d'identifier un peptidique noté $D$ résultant de la réaction entre deux acides $\alpha-$ aminé $A$ et $B$
 
1. Des méthodes d'analyses quantitatives ont permis de déterminer les pourcentages massiques de carbones d'hydrogène et du composé $A$ :
 
Soient : $\%C=40.45$ $\%H=7.87$ $\%N=15.72$
 
1.1 Le composé $A$ ne contenant qu'un atome d'azote par molécule vérifié que sa formule brute s'écrit $C_{3}H_{7}NO_{2}$
 
1.2 Le composé est précisément un acide $\alpha-$ aminé. 
 
Écrire sa formule semi développe et donnez son nom dans la nomenclature officiel
 
2. Par rection de $A$ avec un autre acide $\alpha-$ aminé $B$ de formule brute $C_{5}H_{11}O_{2}$
 
2.1 Écrire la formule semi développé de $B$ sachant que sa molécule deux atomes carbones asymétriques et donnez son nom dans la nomenclature officiel.
 
2.2 Représentez les couples d'énantiomères en utilisant la représentation de Fisher et en précisant les conventions utilisées
 
2.3 Écrire à l'aide de formule développé l'équation bilan traduisant la synthèse du peptide $D$ sachant qu'$A$ est l'acide $\alpha-$ aminé $C-$ terminal. 
 
Encadrer la liaison peptide.
 
3. On effectue une décarboxylation de $A$ par chauffage. 
 
Le composé organique azoté obtenu est dessous dans l'eau pour donner une solution $S.$
 
3.1 Écrire l'équation bilan de la réaction de décarboxylation d'$A.$ 
 
Nommer le produit $E.$
 
3.2 La concentration molaire de $S$ est $C=0.15mole/L$ et son $pH=12.$
 
Déterminer le $pKa$ du couple acide-base correspondant à $E.$
 
3.3 Dans la pratique ce $pKa=11.$
 
Sur un axe gradué en unité de $ph$ placé les domaines de prédominance des diverses formes en justifiant la réponse 

Solution 

1.1.1 Vérifions que la formule brute du composé $A$ s'écrit $C_{3}H_{7}NO_{2}$
 
Soit $C_{x}H_{y}NO_{z}$ la formule brute du composé 
 
On a :
 
$\begin{array}{lcl} \dfrac{12x}{\%C}&=&\dfrac{y}{\%H}\\&=&\dfrac{16z}{\%O}\\&=&\dfrac{14}{\%N}\\&\Rightarrow&x=\dfrac{14\times\%C}{\%N\times 12}\\&=&\dfrac{14\times40.45}{15.72\times 12}\\&\Rightarrow&x=3 \end{array}$
 
$\begin{array}{lcl} y&=&\dfrac{14\times\%H}{\%N\times 1}&=&\dfrac{14\times 7.87}{15.72\times 1}\\&\Rightarrow&y=7 \end{array}$
 
$\begin{array}{lcl} z&=&\dfrac{14\times\%O}{\%N\times 16}&=&\dfrac{14\times(100-(40.45+15.72+7.87))}{15.72\times 16}\\&\Rightarrow&z=2 \end{array}$
 
$\Rightarrow\boxed{C_{3}H_{7}NO_{2}}$
 
1.1.2 Formule semi $-$ développée et nom de l'acide $\alpha-$ aminé dans la nomenclature officiel
 
Il a pour formule semi $-$ développée : $CH_{3}-CH\left(NH_{2}\right)-COOH$ : acide $-2-$ aminopropanoïque 
 
1.2.1.1 Formule semi développé de $B$
 
$C_{2}H_{5}-CH\left(CH_{3}\right)-CH\left(NH_{2}\right)-COOH$ : cide $-2-$ amino $-3-$ méthylpentanoïque 
 
1.2.1.2 Représentation des couples d'énantiomères 
 
 
1.2.2 Équation bilan traduisant la synthèse du peptide $D$ sachant qu'$A$ est l'acide $\alpha-$ aminé $C-$ terminal. 
 
$C_{2}H_{5}-CH\left(CH_{3}\right)-CH\left(NH_{2}\right)-COOH+CH_{3}-CH\left(NH_{2}\right)-COOH\ \longrightarrow\ C_{2}H_{5}-CH\left(CH_{3}\right)-CH\left(NH_{2}\right)-CO-NH-CH\left(CH_{3}\right)-COOH+H_{2}O$
 
3.1 Équation bilan de la réaction de décarboxylation d'$A$
 
$CH_{3}-CH\left(NH_{2}\right)-COOH\stackrel{\Delta}{\longrightarrow}CH_{3}-CH_{2}-NH_{2}+CO_{2}$
 
$E\ :\ CH_{3}-CH_{2}-NH_{2}$ : Ethanamide
 
1.3.2.1 Détermination du $pKa$ du couple acide-base correspondant à $E$
 
La solution d'éthanamide est une solution de base faible 
 
$\begin{array}{lcl} pH&=&\dfrac{1}{2}(pKe+pKa+\log\,C)\\&\Rightarrow&pKa=2pH-pKa-\log\,C\\&=&2\times 12-14-\log\,0.15\\&\Rightarrow&pKa=10.8 \end{array}$
 
1.3.2 Domaines de prédominance des diverses formes 
 
 
Un catalyseur est une substance qui accélère une réaction sans entrer dans le bilan de la réaction et sans modifier l'état final du système. 
 
$-\ $ La catalyse est dite homogène lorsque le catalyseur et le mélange réactionnel constituent une seule phase (forment un mélange homogène). 
 
$-\ $ La catalyse est dite hétérogène lorsque le catalyseur et le milieu réactionnel se trouvent dans des phases différentes. 
 
Les enzymes sont des catalyseurs biologiques qui permettent aux transformations chimiques nécessaires à la vie de s'effectuer à vitesse élevée. 
 
$-\ $ Un catalyseur est sélectif si, à partir d'un système initial susceptible d'évoluer selon plusieurs réactions spontanées, il accélère préférentiellement l'une d'elles.
 
Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Éléments, atomes, classifications des éléments - 2nd S

Classe: 
Seconde
 

I. Éléments

1. Mise en évidence de l'élément carbone

1.1 Pyrolyse du bois

 
La pyrolyse du bois donne du charbon de bois

1.2 Pyrolyse du sucre

La pyrolyse du sucre donne un solide noir appelé charbon de sucre
 
 

1.3 Conclusion

Le charbon de bois (produit de la pyrolyse du bois), le solide noir (résidu de la pyrolyse du sucre) contiennent un constituant commun : le carbone

2. Définition de l'élément chimique

Un élément chimique est un constituant commun à tous les corps qui le contiennent

Remarque

$-\ $ Les corps purs simples sont formés d'un seul élément

Exemples : 

le dihydrogène est formé de l'élément hydrogène ; le dioxygène est formé de l'élément oxygène
 
$-\ $ Les corps purs composés sont formés de plusieurs éléments

Exemples : 

l'oxyde de dihydrogène (eau) est formé de l'élément oxygène et l'élément hydrogène ; le dioxyde de carbone (gaz carbonique) est formé de l'élément oxygène et de l'élément carbone

3. Notation de l'élément chimique

Pour faciliter l'étude de la chimie, les éléments sont représentés par des symboles
 
Généralement, on utilise la première lettre majuscule du nom (français, latin, grec, étranger...)
 
Lorsque plusieurs éléments commencent par la même lettre, on ajoute une seconde lettre minuscule pour les différencier
 
Symboles de quelques éléments chimiques
$$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline \text{Elément}&\text{Hydrogène}&\text{Carbone}&\text{Fer}&\text{Sodium}&\text{Azote}&\text{Oxygène}&\text{Fluor}&\text{Calcium}\\\hline \text{Symbole}&H&C&F&Na&N&O&F&Ca \\ \hline \end{array}$$

II. Atomes

La matière est faite à partir des particules extrêmement petites appelées atomes. 
 
Les propriétés chimiques des corps purs peuvent être interprétées à partir d'un modèle unique d'atome

1. Dimension de l'atome

L'atome est représenté par une sphère infiniment petite.
 
Le diamètre de l'atome est de l'ordre de l'Angstrom $($symbole ; $A^{\circ})$ ; $1\,A^{\circ}=10^{-15}m$

2. Les constituants de l'atome

2.1 Le modèle atomique

L'atome peut être modélisé par une structure présentant un noyau autour duquel existe une zone dans laquelle on peut trouver les électrons. 
 
Cette partie de l'atome est appelée nuage électronique

2.2 Les caractéristiques des constituants de l'atome

 
Les expériences montrent que l'atome est constitué de protons, de neutrons et d'électrons
$$\begin{array}{|c|c|c|} \hline \text{Particule}&\text{Masse}&\text{Charge}\\ \hline \text{Proton}&m_{p}=1.672\cdot10^{-26}kg&q_{n}=1.6\cdot10^{-19}C\\ \hline \text{Neutron}&m_{n}=1.674\cdot10^{-26}kg&q_{n}=0C\\ \hline \text{Electron}&m_{e}=9.1\cdot10^{-31}kg&q_{e}=1.6\cdot10^{-19}C\\ \hline \end{array}$$

Remarque :

$-\ $ La masse $m_{p}=m_{n}=1836\,m_{e}.$
 
La masse des électrons est $1836$ fois plus petite que celle du proton ; donc négligeable par rapport à celle-ci
 
$-\ $ Les charges des protons et des électrons sont identiques et ces particules sont en même nombre dans l'atome ; l'atome est donc électriquement neutre

3. Structure de l'atome

3.1 Le noyau

Le noyau est constitué de deux types de particules : les neutrons et les protons.
 
Ces deux types particules constituants du noyau sont appelés nucléons
 
Chaque atome est caractérisé par :
 
$-\ $ le nombre de protons $Z$ qu'il renferme.
 
Ce nombre est aussi appelé numéro atomique ou nombre de charge
 
$-\ $ le nombre de nucléons $A$ qu'il renferme.
 
Ce nombre est aussi appelé nombre de masse : $A=Z+N$
 
$N$ étant le nombre de neutrons
 
On symbolise le noyau des atomes par :
 
 
$A=Z+N=$ nombre de masse d'un noyau, c'est le nombre de nucléons $($protons $+$ neutrons$)$ qu'il contient.
 
$Z=$ numéro atomique d'un noyau, c'est le nombre de protons qu'il contient.

Exemples : 

$_{6}^{12}C$ ; $_{8}^{16}O$ ; $_{1}^{1}H$ ; $_{7}^{14}N$

Remarque :

Des atomes sont dits isotopes lorsqu'ils renferment le même nombre de protons mais de nombre de nucléons (ou nombre de neutrons) différents

Exemples :

$_{6}^{12}C$, $_{6}^{13}C$ et $_{6}^{14}C$ ;
 
$_{1}^{1}H$, $_{1}^{2}H$ et $_{1}^{3}H$

3.2 Le nuage électronique

3.2.1 Notion du niveau d'énergie

Les électrons d'un atome sont répartis en couche de niveau d'énergie différent. 
 
Pour arracher les électrons d'une même couche, il faut lui fournir la même énergie. 
 
On dit que les électrons d'une même couche ont le même niveau d'énergie
 
Les couches sont désignées par des lettres $K$, $L$, $M$, $N$, $O$, $P$, $Q\ldots.$
 
A chaque couche correspond un nombre entier positif $n$
$$\begin{array}{|c|c|c|c|c|c|c|c|} \hline n&1&2&3&4&5&6&7\\ \hline \text{Lettre}&K&L&M&N&O&P&Q\\ \hline \end{array}$$

3.2.2 Règle de remplissage des couches

La répartition des électrons d'un atome sur les différentes couches ou niveaux d'énergie obéit à deux règles :
 
$-\ $ la première règle ; le nombre maximal d'électrons pouvant à une couche est : $N=2n^{2}$

Exemples :

Couche $K$ : $N=2\times1^{2}\Rightarrow\;N=2$ électrons
 
Couche $L$ : $N=2\times2^{2}\Rightarrow\;N=8$ électrons
 
Couche $M$ : $N=2\times3^{2}\Rightarrow\;N=18$ électrons
 
$-\ $ la deuxième règle ; on remplit successivement les couches dans l'ordre $K$, $L$, $M$, $N\ldots.$
 
Une couche ne commence à se remplir que si la précédente est saturée

3.2.3 La configuration électronique

Pour donner la structure électronique ou la configuration électronique, on représente tous les électrons par des points $(.)$ dans des cases portant autant de places disponibles dans une couche déterminée
 
 

Exemples :

 
 
 

3.2.3 La formule électronique

On écrit la lettre qui correspond à chaque couche et on indique en exposant en haut à droite le nombre d'électrons par couche

Exemples :

$H\;(Z=1)\ :\ K^{1}$ ;
 
$He\;(Z=2)\ :\ K^{2}$ ; 
 
$Li\;(Z=3)\ :\ K^{2}L^{1}$ ; 
 
$C\;(Z=6)\ :\ K^{2}L^{4}$ ; 
 
$O\;(Z=8)\ :\ K^{2}L^{6}$ 
 
$Al\;(Z=13)\ :\ K^{2}L^{8}M^{3}$

3.3 Structure de Lewis d'un atome

La représentation de Lewis permet de mettre en évidence les électrons de la couche externe ou couche périphérique. 
 
Les électrons célibataires sont représentés par des points $(.)$ ; les doublets sont représentés par un tiret $(-)$ placé autour de l'élément considéré

Exemples :

$$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline \qquad\quad\text{Symbole}\qquad&\quad H\quad&\quad C\quad&\quad N\quad&\quad O\quad&\quad P\quad&\quad Cl\quad&\quad Na\quad&\quad Ne\quad\\ \hline \end{array}$$
 

3.4 Valence d'un atome

Le nombre d'électrons célibataires que possède l'élément est la valence
 
 
Hydrogène : monovalent ; Oxygène : divalent ; Azote : trivalent ; Carbone : Tétravalent.

4. Masse de l'atome

La masse $M$ de l'atome est la relation suivante :
 
$M=m_{\text{noyau}}+m_{\text{électrons}}\Rightarrow\ \boxed{M=Zm_{p}+Nm_{n}+Zm_{e}}$
 
Si $m_{p}=m_{n}\Rightarrow\;M=Zm_{p}+Nm_{p}+Zm_{e}$
 
$\Rightarrow M=(Z+N)m_{p}+Zm_{e}\Rightarrow\ \boxed{M=Am_{p}+Zm_{e}}$
 
Si on néglige la masse des électrons $\Rightarrow\ \boxed{M=Am_{p}}$

5. Structure lacunaire de l'atome

La matière de l'atome est essentiellement concentrée dans son noyau. 
 
Les électrons tournent autour du noyau. 
 
Les distances séparant le noyau des électrons sont très grandes. 
 
Ainsi, la plus grandes partie (volume) est constituée de vide. 
 
On dit que l'atome a une structure lacunaire

III. Classification périodique des éléments chimiques

1. Principe de la classification

$-\ $ Les éléments chimiques sont classés par numéro atomique $Z$ croissant ;
 
$-\ $ Les éléments dont les atomes ont le même nombre d'électrons sur leur couche externe sont disposés dans une même colonne verticale et constituent un groupe ou une famille
 
$-\ $ Chaque ligne ou période correspond au remplissage d'une couche électronique

2. Tableau simplifié

Le tableau simplifié comporte trois lignes ou périodes et huit colonnes ou groupe
 
 

3. Intérêt de la classification périodique

Les atomes des éléments de même colonne ont le même nombre d'électrons périphériques. 
 
Ils ont des propriétés chimiques semblables et forment un groupe ou famille
 
Considérons quelques exemples :

3.1 La famille des métaux alcalins

$-\ $ A l'exception de l'hydrogène, les éléments de la première colonne constituent le groupe des alcalins.
 
$-\ $ Ils ont la même structure électronique externe. 
 
Il possède 1 électron sur la couche électronique externe.
 
$Li$ (Lithium) ; 
 
$Na$ (Sodium) ; 
 
$K$ (Potassium)
 
$-\ $ Les corps simples correspondant à ces éléments sont appelés les métaux alcalins.
 
$-\ $ Ce sont des corps mous, légers à l'éclat métallique, très réactifs chimiquement.
 
$-\ $ Ils sont oxydés par le dioxygène de l'air. 
 
Il faut les conserver dans le pétrole, à l'abri de l'air.

3.2 La famille des Halogènes

$-\ $ Les éléments de la $7^{ième}$ colonne constituent la famille des Halogènes. 
 
Ces éléments possèdent la même structure électronique externe à $7$ électrons.
 
$F$ (Fluor) ; 
 
$Cl$ (Chlore) ; 
 
$Br$ (brome) ; 
 
$I$ (iode)
 
$-\ $ Ils existent sous la forme de molécules diatomiques :
 
$-\ $ Le difluor, le dichlore (gaz jaune-vert), le dibrome (liquide jaune-orangé), le diiode (solide violet foncé).

3.3 La famille des gaz nobles

$-\ $ Ce sont les éléments de la dernière colonne.
 
$-\ $ L'Hélium mis à part, ils possèdent une structure externe à huit électrons appelée octet d'électrons.
 
$He$ (Hélium) ; 
 
$Ne$ (Néon) ; 
 
$Ar$ (Argon)
 
$-\ $ Ils possèdent une grande stabilité chimique. 
 
Ce sont des gaz monoatomiques, on les appelle les gaz rares ou gaz inertes

4. Les ions monoatomiques

Certains atomes peuvent perdre ou gagner des électrons et deviennent des ions simples

4.1 Les cations

Un cation ou ion positif provient d'un atome qui a perdu un ou plusieurs électron(s)

Exemples : 

$Na\longrightarrow Na^{+}+e^{-}$ 
 
$Al\longrightarrow Al^{3+}+3e^{-}$ 
 
$B\longrightarrow B^{3+}+3e^{-}$
 
$Mg\longrightarrow Mg^{2+}+2e^{-}$ 
 
$H\longrightarrow H^{+}+e^{-}$ 
 
$Li\longrightarrow Li^{+}+e^{-}$
 
De manière générale : $M\longrightarrow Mn^{+}+ne^{-}$

4.2 Les anions

Un anion ou ion négatif provient d'un atome qui a gagné un ou plusieurs électron(s)

Exemples : 

$Cl^{+}e^{-}\longrightarrow Cl^{-}$
 
$P+3e^{-}\longrightarrow P^{3-}$
 
$N+3e^{-}\longrightarrow N^{3-}$
 
$Mg+2e^{-}\longrightarrow Mg^{2-}$ 
 
$F+e^{-}\longrightarrow F^{-}$ 
 
$H+e^{-}\longrightarrow H^{-}$
 
De manière générale : $M+ne^{-}\longrightarrow M^{n-}$
 
Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Cinématique - Ts

Classe: 
Terminale

Exercice 1

Un mobile $M_{1}$ est en mouvement relativement au repère d'espace $\mathcal{R}(O\;,\ \vec{i}\;,\ \vec{j})$, son vecteur vitesse est : $\overrightarrow{V}_{1}=3\vec{i}+(-2t+4)\vec{j}$
 
1) Donner les lois horaires du mouvement sachant qu'à l'origine des temps, le mobile passe par l'origine $O.$
 
2) Établir l'équation cartésienne de la trajectoire.
 
3) Établir l'expression du vecteur accélération $\overrightarrow{\alpha}_{1}.$
 
Le représenter sur la trajectoire de la figure.
 
 
4) A quelle date la direction du vecteur vitesse est horizontale ? 
 
En déduire les coordonnées $(x_{s}\ ;\ y_{s})$ du sommet S de la trajectoire ainsi que la valeur de la vitesse en ce point.
 
Représenter ce vecteur vitesse.
 
5) Calculer :
 
Le rayon de courbure de la trajectoire à la date $t=2s.$
 
L'abscisse $x_{p}$ du mobile lorsque celui-ci repasse par l'ordonnée $y=0.$
 
La valeur de la vitesse $\overrightarrow{V}_{p}$ du mobile en ce point.
 
6) Un deuxième mobile $M_{2}$ en mouvement rectiligne uniformément varié sur l'axe $(ox)$ du repère $\mathcal{R}(O\;,\ \vec{i}\;,\ \vec{j})$, passe par le point d'abscisse $x=20\,m$ à l'instant $t=0$ avec une vitesse $\overrightarrow{V}_{O_{2}}=2\vec{i}$
 
Déterminer la valeur algébrique de l'accélération du mobile $M_{2}$ au point du rencontre avec $M_{1}$ pour $x=12\;m$

Exercice 2

Dans un repère $(O\;,\ \vec{i}\;,\ \vec{j})$ orthonormé, les lois horaires du mouvement d'un mobile ponctuel $M$ sont données par : $x=t$ et $y=\dfrac{t^{2}}{2}$ le temps est mesuré en secondes et les distances en mètres. 
 
A $t=0s$ le mobile débute son mouvement.
 
1) a) Quel est le point de départ du mobile à l'origine des dates ?
 
b) Établir l'équation de la trajectoire du mobile relativement au repère $(O\;,\ \vec{i}\;,\ \vec{j}).$
 
c) Déterminer l'expression du vecteur vitesse et celle du vecteur accélération du mobile $M.$
 
2) a) A quelle date le vecteur vitesse est colinéaire à $\vec{i}$ ?
 
b) Montrer qu'à cette date la composante tangentielle de l'accélération est nulle.
 
3) Sachant, qu'à une date $t$, l'accélération tangentielle a pour expression $\alpha_{T}=\dfrac{t}{\sqrt{1+t^{2}}}$ dans le repère de Frenet $(M\;,\ \overrightarrow{T}\;,\ \overrightarrow{N})$.
 
a) Montrer que celle de l'accélération normale est $\alpha_{N}=\dfrac{1}{\sqrt{1+t^{2}}}.$
 
b) A quelle date $t_{1}$, $V_{x}=V_{y}$ avec $V_{x}$ et $V_{y}$ les composantes du vecteur vitesse dans le repère $(O\;,\ \vec{i}\;,\ \vec{j})$ ?
 
c) Calculer le rayon de courbure à la date $t_{1}.$

Exercice 3

Dans un repère $\mathcal{R}=(O\;,\ \vec{i}\;,\ \vec{j})$, un point mobile $M_{1}$ est animé d'un mouvement rectiligne uniformément varié d'accélération $a_{1}=-2\,m\cdot s^{-1}.$ 
 
A la date $t_{1}=1\,s$, le mobile $M_{1}$ passe par le point $A$ d'abscisse $x_{A}=0\,m$ avec une vitesse $V_{A}=6\,m\cdot s^{-1}.$ 
 
Sachant que le mobile débute son mouvement à la date $t=0s.$
 
1) Déterminer la vitesse initiale et l'abscisse initiale du point mobile $M_{1}.$
 
2) Écrire la loi horaire $x_{1}(t)$ de mouvement de $M_{1}.$ 
 
Déduire l'expression de sa vitesse instantanée.
 
3) Montrer que le mouvement de $M_{1}$ comporte deux phases.
 
4) Calculer la distance parcourue par le mobile entre les dates $t_{1}=1\,s$ et $t_{2}=7\,s.$

Exercice 4

Les équations horaires du mouvement d'un mobile $M$ relativement à un repère d'espace $\mathcal{R}$ $(O\;,\ \vec{i}\;,\ \vec{j})$ sont $x=2t$ et $y=f(t)$  $(t>0).$ 
 
L'équation cartésienne de la trajectoire est $y=-\dfrac{5}{4}x^{2}+2x.$
 
1) Représenter l'allure de la trajectoire.
 
2) Déterminer l'expression de l'ordonnée $y=f(t)$ du mobile.
 
2) a) Déterminer les composantes du vecteur vitesse $\overrightarrow{V}$ en fonction du temps.
 
2) b) à quelle date la direction du vecteur vitesse est horizontale, en déduire les coordonnées du sommet $S$ de la trajectoire. 
 
Calculer la valeur de la vitesse en ce point.
 
3) Donner l'expression du vecteur accélération $\vec{a}.$
 
Conclure.
 
4) Calculer le rayon de courbure de la trajectoire au sommet $S$ de la trajectoire.
 
5) Déterminer les phases du mouvement.
 
6) Déterminer l'abscisse du point $P$ $(P\neq O)$ intersection de la trajectoire avec l'axe $ox.$
 
Quelles sont les caractéristiques du vecteur vitesse $\overrightarrow{V}_{p}$ en ce point ? 
 
Comparer ce vecteur au vecteur $\overrightarrow{V}_{O}$ (direction, valeur). 
 
Représenter ces deux vecteurs sur la trajectoire. 
 
(Échelle de votre choix).

Exercice 5

Un mobile $M$ décrit une trajectoire rectiligne dans un repère $(O\ ;\ \vec{i})$ ; son vecteur accélération est constant pendant toute la durée de son mouvement dans l'intervalle de temps $[0\ ;\ 5s].$
 
A l'origine du temps, le mobile $M$ part de la position d'abscisse $x_{0}=0.5\,m$ avec une vitesse $v_{0}=-1\,m\cdot s^{-1}$, puis il passe par le point d'abscisse $x_{1}=5m$ avec une vitesse $v_{1}=4.7\,m\cdot s^{-1}.$
 
1) Calculer l'accélération $a$ du mouvement.
 
2) Établir l'expression de la vitesse instantanée $v(t)$ du mobile.
 
3) Déduire l'instant pour lequel le mobile passe par le point d'abscisse $x_{1}.$
 
4) Établir l'équation horaire du mouvement.
 
5) Après deux secondes du départ du mobile $M$, un deuxième mobile $M'$ part du point d'abscisse $x=5m$, en mouvement rectiligne uniforme de vitesse $v'=4m\cdot s^{-1}.$
 
a) Déterminer l'équation horaire du mouvement du mobile $M'$
 
b) Calculer la date $t$ de rencontre des mobiles.
 
c) Calculer l'abscisse $x$ correspondant à cette rencontre.

Exercice 6

Un mobile parcourt une distance $AB=300m$ en deux phases.
 
$-\ $ $1^{ière}$ phase : mouvement rectiligne uniformément accéléré d'accélération $a_{1}=2\,m\cdot s^{-2}$
 
$-\ $ $2^{ième}$ phase : mouvement rectiligne uniformément retardé d'accélération $a_{2}=-1m\cdot s^{-2}.$ 
 
A $t=Os$ le mobile part du point $A$, pris comme origine des espaces, sans vitesse initiale et arrive au point $B$ avec une vitesse nulle
 
 
1) Soit $C$ le point ou le mouvement devient retardé :
 
a) Exprimer, pour la $1^{ière}$ phase, $x_{C}$ en fonction de $V_{C}$ et $a_{1}.$
 
b) Exprimer, pour la $2^{ième}$ phase, $V_{C}$ en fonction de $a_{2}$, $x_{B}$ et $x_{C}.$
 
c) Déduire d'après a) et b) l'expression de $V_{C}$ en fonction de $a_{1}$, $a_{2}$ et $x_{B}.$
 
Calculer sa valeur
 
2) a) Calculer la distance parcourue $AC$ pendant la $1^{ière}$ phase.
 
b) Calculer sa durée.
 
3) a) Déduire la distance parcourue $CB$ pendant la $2^{ième}$ phase.
 
b) Calculer la durée du trajet $AB.$

Exercice 7

Un solide supposé ponctuel est attaché à un ressort à l'instant $t=0s$ ; le solide est ramené au point d'abscisse $x_{0}$ ; on lui communique une vitesse $\overrightarrow{V}_{0}$ et on l'abandonne à lui-même, il effectue donc un mouvement rectiligne sinusoïdal dont l'enregistrement est donné par la figure suivante.
 
 
1) a) En exploitation l'enregistrement déterminer :
 
$-\ $ la pulsation du mouvement $\omega.$
 
$-\ $ l'élongation initiale $x_{0}.$
 
$-\ $ l'amplitude $X_{m}.$
 
$-\ $ la phase initiale $\varphi.$
 
b) En déduire la loi horaire $x=f(t).$
 
2) a) Déterminer l'expression de la vitesse en fonction du temps.
 
b) En déduire la valeur algébrique de la vitesse initiale $\overrightarrow{V}_{0}.$
 
3) A l'instant $t_{1}>0$ ; le mobile repasse pour la première fois par la position d'abscisse $x_{0}$ dans le sens négatif.
 
a) Déterminer graphiquement $t_{1}.$
 
b) Retrouver $t_{1}$ par le calcul.
 
4 Déterminer la valeur algébrique de la vitesse du solide lors de son premier passage par la position d'abscisse $x=2\,cm.$

Exercice 8

Un point mobile $M$ est animé d'un mouvement circulaire accélération angulaire est $\ddot{\theta}=-\dfrac{\pi}{5}rad\cdot s^{-2}$ entre les instants $t_{0}=0s$ et $t_{1}=20s$. 
 
Le rayon de sa trajectoire est $R=25\,cm.$
 
A l'origine des dates, $M$ part de la position d'abscisse angulaire $\dfrac{\pi}{3}$ avec une vitesse angulaire initiale $\dot{\theta}_{0}=2\pi\;rad\cdot s^{-1}.$
 
1) Quelle est la nature de mouvement du mobile.
 
2) Donner les expressions de sa vitesse angulaire $\dot{\theta}$ et de son élongation angulaire $\theta$ en fonction du temps.
 
3) a) Montrer que ce mouvement comporte deux phases.
 
b) Déterminer le nombre de tours effectué par le mobile pendant la première phase du mouvement.
 
4) Calculer à la date $t_{1}$
 
a) La vitesse angulaire $\dot{\theta}_{1}$ ainsi que la vitesse linéaire du mobile.
 
b) l'accélération normale et l'accélération tangentielle du mobile. 
 
Déduire la valeur de son accélération linéaire.
 
5) A partir de la date $t_{1}$, le mouvement du mobile $M$ est circulaire uniforme à la vitesse angulaire $\dot{\theta}_{1}.$ 
 
Calculer :
 
a) La période de ce mouvement. 
 
Déduire sa fréquence.
 
b) Montrer que l'accélération linéaire d'un mouvement circulaire uniforme est égale à l'accélération normale.

Exercice 9

Une automobile se déplace sur une route horizontale à la vitesse constante de valeur $\|\overrightarrow{V}_{0}\|=16\,m\cdot s^{-1}.$
 
Lorsqu'elle est à une distance $d=200\,m$ du feu, le feu vert s'allume et reste pendant $11s.$
 
Dans tout l'exercice, on prendra comme origine des temps $(t=0s)$, l'instant où le feu vert s'allume et l'origine des espaces $(x_{0}=0\,m)$, la position de la voiture à cet instant. 
 
Le sens positif est le sens du mouvement.
 
 
1) A partir de l'instant de date $t=0s$, l'automobiliste accélère et impose à sa voiture une accélération constante. 
 
A l'instant $t_{1}$, sa vitesse prend la valeur $v_{1}=21\,m\cdot s^{-1}.$
 
Entre $t=0s$ et $t_{1}$, l'automobiliste parcourt $100\,m.$
 
a) Déterminer l'accélération $a_{1}.$
 
b) Déterminer la date $t_{1}.$
 
c) Écrire la loi horaire du mouvement de la voiture pour $t\in[0\;,\ t_{1}].$
 
2) A partir de l'instant $t_{1}$, l'automobiliste maintient sa vitesse constante.
 
a) Écrire la loi horaire du mouvement de la voiture pour $t\geq t_{1}.$
 
b) La voiture passe-t-elle devant le feu lorsqu'il est vert ? 
 
Justifier la réponse
 
3) Si l'instant $t_{1}$, l'automobiliste freine et impose à sa voiture un mouvement uniformément retardé d'accélération $a_{2}=-2\,m\cdot s^{-2}$
 
a) Calculer la distance parcourue par la voiture du début de freinage jusqu'à son arrêt
 
b) Déterminer la vitesse $v_{2}$ de la voiture en passant devant le feu et la date $t_{2}$ correspondante à ce passage.
 
c) Vérifier que la voiture est passée lorsque le feu n'est plus vert.
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 
Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Mélanges et corps purs - 2nd S

Classe: 
Seconde
 
 
Tous les objets qui nous entourent (êtres vivants, végétaux, minéraux...) constituent la matière
 
Les roches, les arbres, l'air...etc, ont des exemples de matières

I. Les états physiques de la matière et changements d'états

1. États physiques de la matière

La matière se présente dans la nature sous trois états différents : l'état solide, l'état liquide et l'état gazeux

1.1 L'état solide

A l'état solide, un corps possède une forme et un volume propres
 
Les solides sont incompressibles
 
Moyennant un effort, on peut changer la forme d'un solide, mais il est pratiquement impossible de faire varier son volume
 
Certains solides sont élastiques, mais chaque solide à sa limite d'élasticité

Exemples : 

cahier, bois, fer, charbon...
 
 

1.2 L'état liquide

Les liquides n'ont pas de forme propre, mais leur volume est invariable ; ils sont fluides et incompressibles

Exemples : 

l'eau, pétrole, l'essence, le lait...
 
 

Remarque

Les solides en poudre, divisés ou pulvérisés s'écoulent comme les liquides, mais leur surface libre n'est ni plane, ni horizontale comme les liquide

1.3 L'état gazeux

Les gaz n'ont pas de forme propre, ni de volume propre. 
 
Ils sont compressibles, expansibles et élastiques. 
 
Ils sont fluides

Exemples : 

l'air, le dioxyde de carbone, le dioxygène...
 
 

Remarque :

Les solides sont caractérisés par un état ordonné et compact. 
 
L'état liquide est désordonné.
 
L'état physique des gaz est désordonné et diffus

2. Les changements d'état physique

2.1 Définition

Le passage d'un état physique à un autre état physique est appelé changement d'état

2.2 Digramme de changement d'état

Un changement d'état physique s'effectue toujours à une température constante sous une pression donnée
 
 

3. Les transformations de la matière

3.1 Phénomène physique

Un phénomène physique est une transformation au cours de laquelle la nature de la matière n'est pas altérée (dénaturée ou détruite)

Exemples : 

la fusion de la glace ; la dilatation des métaux ; la rosée...

3.2 Phénomène chimique

Un phénomène chimique est une transformation au cours de laquelle la nature de la matière est altérée (dénaturée ou détruite)

Exemples : 

Action de l'eau de Javel sur une tache ; la décomposition de la craie par un acide ; feuille de papier brulée

II. Les mélanges

1. Définition

Un mélange est un ensemble de deux ou plusieurs constituants
 
Il peut être solide, liquide ou gaz

2. Mélange hétérogène

Un mélange hétérogène est un mélange dans lequel on peut distinguer à l' œil nu ses différents constituants

Exemples : 

eau $+$ huile ; eau $+$ terre ; boissons gazeuses
 
 

3. Mélange homogène

Un mélange homogène est un mélange dans lequel on ne peut pas distinguer à l' œil nu ses différents constituants

Exemples : 

lait ; sirop ; thé
 
 

4. Méthodes de séparation des constituants d'un mélange

Il existe de nombreuses méthodes variables de séparation selon la nature du mélange et la nature des constituants qui le constituent.
 
Parmi ces méthodes, on citer :

4.1 La décantation

La décantation est une de séparation qui consiste à laisser le mélange au repos pour que les particules solides lourdes se déposent au fond du récipient. 
 
En transvasant, on peut séparer le liquide de ces particules.
 
Le produit de la décantation est appelé décantat

Exemples de décantation

$-\ $ Décantation d'un mélange solide-liquide : jus d'orange
 
 
$-\ $ Décantation d'un mélange liquide-liquide :
 
 

4.2 La filtration

La filtration est une méthode de séparation qui consiste à faire passer le mélange liquide à travers un filtre .
 
Le produit de la filtration est appelé filtrat
 
 

4.3 La distillation

La distillation est une méthode de séparation basée sur la différence de température d'ébullition.
 
Elle consiste à vaporiser partiellement un mélange liquide homogène et à condenser les vapeurs formées pour les séparer
 
Le produit de la distillation est appelé distillat

Exemple : 

distillation de l'eau sucrée
 
 

Remarque :

Pour séparer les différents constituants de l'air, on le liquéfie en le comprimant. 
 
On procède alors à la distillation de ce liquide
 
Au début de l'ébullition (température de liquéfaction du diazote liquide $(-196^{\circ}C)$, il se dégage du diazote, puis le dioxygène lorsque la température atteint $-183^{\circ}C$ (température de liquéfaction du dioxygène)
 
L'air est donc un mélange dont l'expérience montre qu'il est constitué de $78\%$ de diazote $(4/5$ en volume$)$, de $21\%$ de dioxygène $(1/5$ en volume$)$ et $1\%$ d'autres gaz (gaz rares, dioxyde de carbone et de la vapeur d'eau)

4.4 Quelques autres méthodes de séparation

4.4.1 La congélation


C'est une méthode de séparation basée sur la différence de cristallisation (température à laquelle un corps se congèle).
 
Le corps dont sa température d'ébullition est plus grande est récupéré le premier sous formes de cristaux

4.4.2 Le tamisage

Si les grains de différents solides ont des dimensions différentes, le passage au tamis permet de les séparer

4.4.3 La flottation

On mouille le mélange. 
 
Selon le liquide choisi, certaines particules flottent

4.4.4 Le triage magnétique

Si un des constituants du mélange contient du fer, les particules de ce constituant sont attirées par l'aimant

III. Corps purs

1. Définition

Un corps pur est un corps qu'on ne peut pas fractionner par une méthode quelconque de séparation
 
2. Critères de pureté d'un corps pur
 
Tout corps pur est défini par les constantes physiques parmi lesquelles on citer :
 
$-\ $ la masse volumique
 
$-\ $ les points de changement d'état : température de fusion, d'ébullition, de solidification etc...

Exemple : 

Valeurs de quelques constantes physiques de l'eau pure.
 
$-\ $ masse volumique : $1kg/L$
 
$-\ $ température de solidification ou de fusion : $t=0^{\circ}C$
 
$-\ $ température d'ébullition ou de liquéfaction : $t=100^{\circ}C$

3. Corps purs simples et corps purs composés

3.1 Analyse de l'eau

3.1.1 Définition

Analyser un corps revient à chercher ses constituants par une méthode appropriée

3.1.2 L'électrolyse de l'eau

 
Mettons de l'eau additionnée de quelques gouttes d'acide dans le voltamètre (ou cuve à l'électrolyse) et fermons l'interrupteur
 
On constate que le courant circule et des dégagements gazeux au niveau des tubes
 
A l'anode $($signe $+)$, le gaz recueilli rallume une buchette presque éteinte. 
 
Ce gaz est le dioxygène
 
 
A la cathode $($signe $-)$, le gaz recueilli a volume deux fois grand et produit une légère détonation en présence d'une allumette enflammée. 
 
Ce gaz est le dihydrogène
 
 

Conclusion :

$-\ $ L'eau est décomposé par le courant électrique en dioxygène et en dihydrogène
 
$-\ $ Le volume de dihydrogène est le double du volume de dioxygène : dihydrogène dioxygène $V_{\text{dihydrogène}}=2V_{\text{dioxygène}}$
 
$-\ $ La masse totale des gaz (dihydrogène et dioxygène) est égale à la d'eau disparue : $m_{e}=m_{H}+m_{O}$
 
eau $\longrightarrow$ dioxygène $+$ dihydrogène
$18g$             $16g$                       $2g$
 
Les masses de dihydrogène et de dioxygène sont proportionnelles à la masse d'eau disparue
 
$\dfrac{m_{H}}{m_{E}}=\dfrac{2g}{18g}\Rightarrow\ m_{H}=\dfrac{1}{9}m_{E}$
 
$\dfrac{m_{O}}{m_{E}}=\dfrac{16g}{18g}\Rightarrow\ m_{O}=\dfrac{8}{9}m_{E}$
 
$-\ $ Un corps pur qui peut décomposer en deux ou plusieurs corps purs est un corps pur composé

Exemple : 

l'eau
 
$-\ $ Un corps pur qui ne peut être décomposé en d'autres corps purs est un corps simple

Exemples : 

le dioxygène et le dihydrogène

3.2 Synthèse de l'eau

3.2.1 Définition

La synthèse de l'eau est la formation de l'eau à partir du mélange du dihydrogène et du dioxygène.

3.2.2 Synthèse eudiométrique

 
On déclenche des étincelles électriques au niveau des électrodes pour amorcer le processus de synthèse
 
$-\ $ La pression des gaz baisse, le niveau de mercure qui va remonter lorsque les deux gaz réagissent en formant une buée (eau) sur la paroi interne du tube eudiométrique.
 
dioxygène $+$ dihydrogène $\longrightarrow$ eau
 $16g$                $2g$                $18g$        
 
La masse d'eau produite est proportionnelle à la masse de dihydrogène ou à la masse de dioxygène
 
$\dfrac{m_{E}}{m_{H}}=\dfrac{18g}{2g}\Rightarrow\ m_{E}=9m_{H}$
 
$\dfrac{m_{E}}{m_{O}}=\dfrac{18g}{16g}\Rightarrow\ m_{E}=\dfrac{9}{8}m_{O}$
 
Auteur: 
Sidy Mouhamed Ndiaye

Acides et bases faibles - Dosage des acides faibles et des base faibles - Ts

Classe: 
Terminale
 

A. Acides faibles et base faibles

I. Théorie de Bronsted

1. Acide

Un acide est une entité chimique capable de céder au moins un proton $H^{+}$

Exemples :

$CH_{3}-COOH\rightarrow CH_{3}-COO^{-}+H^{+}$
 
$NH_{4}^{+}\rightarrow NH_{3}+H^{+}$
 
$H_{2}O\rightarrow OH^{-}+H^{+}$

2. Base

Une base est une entité chimique susceptible de capter au moins un proton $H^{+}$

Exemples :

$CH_{3}-COO^{-}+H^{+}\rightarrow CH_{3}-COOH$
 
$NH_{3}+H^{+}\rightarrow NH_{4}^{+}$
 
$H_{2}O+H^{+}\rightarrow H_{3}O^{+}$

3. Couple acide-base

Les exemples ci-dessus montre qu'à tout acide est associé une base et vice-versa 
 
L'acide et la base associée sont dits conjugués.
 
On dit qu'ils constituent un couple acide-base.
 
Le caractère acide d'une espèce peut être schématisé par l'écriture : $A\ \rightarrow\ B\ +\ H^{+}$
 
Le caractère basique d'une espèce peut être schématisé par l'écriture : $B\ +\ H^{+}\ \rightarrow\ A$
 
Le couple acide-base est noté par convention dans l'ordre $A|B.$
 
On peut traduire le transfert de proton entre les deux formes acide-base par l'équilibre formel : $A\ \leftrightarrows\ B+H^{+}$

Remarque :

L'eau est à la fois acide et base.
 
On dit que l'eau est une espèce amphotère (ou que l'eau est un amphotère ou ampholyte)

Exemples de couples acide-base

$CH_{3}CCOOH|CH_{3}CCOO^{-}$
 
$NH_{4}^{+}|NH_{3}$
 
$H_{2}O|OH^{-}$
 
$H_{3}O^{+}|H_{2}O$

II. Acides faibles

1. Étude d'un exemple : solution d'acide éthanoïque $CH_{3}COOH$

On prépare une solution d'acide éthanoïque $CH_{3}COOH$ de concentration de $C=10^{-1}mol\cdot L^{-1}$
 
La mesure du $pH$ à l'aide de $pH-$ mètre donne une valeur égale $pH=2.9$
 
Étudions la solution aqueuse de l'acide éthanoïque
 
Les espèces chimiques présentes dans la solution : $H_{3}O^{+}$, $CH_{3}COO^{-}$, $OH^{-}$ et éventuellement des molécules de $CH_{3}COOH$ non ionisées 
 
$pH=2.9\Rightarrow\left[H_{3}O^{+}\right]=1.26\cdot 10^{-3}mol\cdot L^{-1}$
 
Le produit ionique s'écrit :
 
$\begin{array}{lcl} Ke&=&\left[H_{3}O^{+}\right]\left[OH^{-}\right]\\&\Rightarrow&\left[OH^{-}\right]=\dfrac{Ke}{\left[H_{3}O^{+}\right]}\\&=&\dfrac{10^{-14}}{1.26\cdot 10^{-3}}\\&\Rightarrow&\left[OH^{-}\right]=7.94\cdot 10^{-12}mol\cdot L^{-1} \end{array}$ 
  
L'électroneutralité de la solution s'écrit :
 
$\begin{array}{lcl} \left[H_{3}O^{+}\right]&=&\left[OH^{-}\right]+\left[CH_{3}COO^{-}\right]\\&\Rightarrow&\left[CH_{3}COO^{-}\right]=\left[H_{3}O^{+}\right]-\left[OH^{-}\right]\\&=&1.26\cdot 10^{-3}-7.94\cdot 10^{-12}\\&\Rightarrow&\left[CH_{3}COO^{-}\right]=1.26\cdot 10^{-3}mol\cdot L^{-1} \end{array}$ 
 
La conservation de la matière s'écrit :
 
$\begin{array}{lcl} \left[CH_{3}COOH\right]_{i}&=&\left[CH_{3}COOH\right]_{d}+\left[CH_{3}COOH\right]_{r}\\&\Rightarrow&\left[CH_{3}COOH\right]_{r}=\left[CH_{3}COOH\right]_{i}-\left[CH_{3}COOH\right]_{d}\\&\Rightarrow&\left[CH_{3}COOH\right]_{r}=C-\left[CH_{3}COO^{-}\right]\\&=&10^{-1}-1.26\cdot10^{-3}\\&\Rightarrow&\left[CH_{3}COOH\right]_{r}=9.87\cdot10^{-2}mol\cdot L^{-1} \end{array}$ 
 
Des molécules d'acide éthanoïque $CH_{3}COOH$ existent en solution
 
La réaction entre l'acide éthanoïque et l'eau n'est pas donc totale et l'on écrit :
$$CH_{3}COOH\ +\ H_{2}O\ \leftrightarrows\ H_{3}O^{+}\ +\ CH_{3}COO^{-}$$
 
La réaction entre l'acide éthanoïque $CH_{3}COOH$ et l'eau n'étant pas totale, on dit que $CH_{3}COOH$ est un acide faible

2. Solutions d'acides faibles

2.1 Définition

Un acide faible est une espèce chimique qui s'ionise partiellement dans l'eau pour donner des ions hydronium $H_{3}O^{+}$
 
L'équation-bilan de la réaction s'écrit :
$$AH\ +\ H_{2}O\ \leftrightarrows\ H_{3}O^{+}\ +\ A^{-}\quad\text{ou}$$
$$A\ +\ H_{2}O\ \leftrightarrows\ B\ +\ H_{3}O^{+}\quad\text{ou}$$
$$BH^{+}\ +\ H_{2}O\ \leftrightarrows\ B\ +\ H_{3}O^{+}$$

2.2 Exemples d'acides faibles

$CH_{3}COOH\qquad\ NH_{4}^{+}$
 
$H_{2}O\qquad\ H_{3}O^{+}$
 
Tous les acides carboxyliques sont des acides faibles

III. Bases faibles

1. Étude d'un exemple : solution d'ammoniac

On dispose d'une solution aqueuse d'ammoniac de $C=10^{-1}mol\cdot L^{-1}$ ; son $pH$ est égal à $11.1$
 
Étudions la solution aqueuse d'ammoniac
 
Les espèces chimiques présentes dans la solution sont : $NH_{4}^{+}$, $OH$, $H_{3}O^{+}$ et éventuellement $NH_{3}$ non dissociée 
$\begin{array}{lcl} pH&=&11.1\\&\Rightarrow&\left[H_{3}O^{+}\right]=10^{-11.1}\\&\Rightarrow&\left[H_{3}O^{+}\right]=7.94\cdot10^{-12}mol\cdot L^{-1} \end{array}$
 
Le produit ionique de l'eau s'écrit :
 
$\begin{array}{lcl} Ke&=&\left[H_{3}O^{+}\right]\left[OH^{-}\right]\\&\Rightarrow&\left[OH^{-}\right]=\dfrac{Ke}{\left[H_{3}O^{+}\right]}\\&=&\dfrac{10^{-14}}{7.94\cdot10^{-12}}\\&\Rightarrow&\left[OH^{-}\right]=1.26\cdot10^{-3}mol\cdot L^{-1} \end{array}$
 
L'électroneutralité de la solution  s'écrit :
 
$\begin{array}{lcl} \left[H_{3}O^{+}\right]+\left[NH_{4}^{+}\right]&=&\left[OH^{-}\right]\\&\Rightarrow&\left[NH_{4}^{+}\right]=\left[OH^{-}\right]-\left[H_{3}O^{+}\right]=1.26\cdot10^{-3}-7.94\cdot10^{-12}\\&\Rightarrow&\left[NH_{4}^{+}\right]=1.26\cdot10^{-3}mol\cdot L^{-1} \end{array}$
 
La conservation de la matière s'écrit :
 
$\begin{array}{lcl} \left[NH_{3}\right]_{i}+&=&\left[NH_{3}\right]_{d}+\left[NH_{3}\right]_{r}\\&\Rightarrow&\left[NH_{3}\right]_{r}=\left[NH_{3}\right]_{i}-\left[NH_{3}\right]_{d}\\&=&C-\left[NH_{4}^{+}\right]\\&=&10^{-1}-1.26\cdot10^{-3}\\&\Rightarrow&\left[NH_{3}\right]_{r}=9.87\cdot10^{-2}mol\cdot L^{-1} \end{array}$
 
Des molécules d'ammoniac $NH_{3}$ existent en solution 
 
La réaction entre l'ammoniac $NH_{3}$ et l'eau n'est pas donc totale et l'on écrit :
$$NH_{3}\ +\ H_{2}O\ \leftrightarrows\ NH_{4}^{+}\ +\ OH^{-}$$
 
La réaction entre l'ammoniac $NH_{3}$ et l'eau n'étant pas totale, on dit que $NH_{3}$ est une base faible

2. Solutions aqueuses de bases faibles

2.1 Définition

Une base faible est une espèce chimique qui s'ionise partiellement dans l'eau  pour donner des ions hydroxyde $OH^{-}$
 
L'équation-bilan de la réaction s'écrit :
 
$A^{-}\ +\ H_{2}O\ \leftrightarrows\ OH^{-}\ +\ AH\quad\text{ou}\quad B\ +\ H_{2}O\ \leftrightarrows\ A\ +\ OH^{-}$

2.2 Exemples de bases faibles

$CH_{3}CCOONa\qquad NH_{3}$
 
$H_{2}O\qquad CH_{3}NH_{3}$
 
Toutes les amines sont des bases faibles

Remarque :

Un acide faible ou une base faible peut être caractérisé (e) par un coefficient de dissociation (ou d'ionisation) appelé coefficient de dissociation ou (d'ionisation) noté $\alpha$
 
$\alpha=\dfrac{C}{C_{0}}$
 
$C$ : concentration de l'acide ou de la base ionisé(e)
 
$C_{0}$ : concentration initiale de l'acide ou de la base 
 
Le coefficient de dissociation $\alpha$ de l'acide faible ou de la base faible s'exprime aussi en fonction du $pH$
 
Pour un acide $\alpha=\dfrac{\left[H_{3}O^{+}\right]}{C}=\dfrac{10^{-pH}}{C}$
 
Pour une base $\alpha=\dfrac{\left[OH^{-}\right]}{C}=\dfrac{10^{(pH-14)}}{C}$

IV. Constante d'acidité

1. Constante de réaction

Lorsqu'une réaction peut être s'effectuer dans les deux sens, il correspond une grandeur appelée constante de réaction notée $K$
 
Soit l'équilibre : 
$$A\ +\ B\ \leftrightarrows\ C\ +\ D$$
$$K=\dfrac{[C][D]}{[A][B]}$$
 
La constante de cette réaction  est :
    
Cette constante de réaction ne dépend que de la température

2. Constante de réaction réduite ou constante d'acidité $K_{A}$

Lorsque l'un des réactifs ou l'un des produits est très excès par rapport aux autres (c'est le cas de l'eau pour les solutions diluées), on définit une constante d'équilibre réduite $Kr$ appelée constante d'acidité $K_{A}$
 
$-\ $ Exemples :
 
$CH_{3}COOH+H_{2}O\ \leftrightarrows\ CH_{3}COO^{-}+H_{3}O^{+}$
 
$\Rightarrow\;K_{A}=\dfrac{\left[H_{3}O^{+}\right]\left[CH_{3}COOH\right]}{\left[CH_{3}COOH\right]}$
 
$NH_{4}^{+}+H_{2}O\ \leftrightarrows\ NH_{3}+H_{3}O^{+}$
 
$\Rightarrow\;K_{A}=\dfrac{\left[H_{3}O^{+}\right]\left[NH_{3}\right]}{\left[NH_{4}^{+}\right]}$
 
$-\ $ Généralisation 
 
Pour un couple acide-base quelconque
 
 

3. Utilisation de l'indicateur coloré

L'utilisation de l'indicateur coloré permet dans certains cas d'effectuer le dosage acido-basique : il doit être judicieusement choisi de manière à changer la couleur lorsqu'on atteint l'équivalence

Choix de l'indicateur coloré :

Lors d'un dosage colorimétrique, il faut choisir l'indicateur coloré dont la zone de virage contient le $pH$ du point d'équivalence

V. Les solutions tampons

1. Définition

Une solution tampon est une solution dont le $pH$ très peu sensible à la dilution et varie peu lors de l'addition des quantités modérées d'un acide fort ou d'une base forte 

2. Réalisation des solutions tampons

Une solution tampon s'obtient en mélangeant un acide faible et sa base conjuguée de façon à obtenir des concentrations voisines
 
On peut également faire réagir l'une des espèces pour fabriquer son conjugué de sorte que les concentrations de la forme acide et de la forme soient égales comme lors de la demi-équivalence du dosage
 
L'efficacité du tampon réalisé est maximale lorsque les concentrations des deux espèces du couple sont égales, c'est-à-dire lorsqu'on a :
 
$-\ $ soit $[AH]=[A^{-}]$ pour le couple $AH|A^{-}$
 
$-\ $ soit $[BH^{+}]=[B]$ pour le couple $BH^{+}|B$
 
Dans ces conditions $pH=pK_{A}$

Remarque :

Lorsqu'on ajoute un acide, les ions  $H_{3}O^{+}$ qu'il fournit disparaissent en réagissant avec la base présente :
$$H_{3}O^{+}\ +\ A\ \longrightarrow\ H\ +\ H_{2}O$$
 
Lorsqu'on ajoute une base, c'est l'acide conjugué qui intervient pour consommer les ions $OH^{-}$ apportés par la base :
$$AH\ +\ OH^{-}\ \longrightarrow\ A^{-}\ +\ H_{2}O$$

3. Importance des solutions tampons

Les solutions tampons peuvent servir à :
 
$-\ $ l'étalonnage d'un $pH-$ mètre,
 
$-\ $ l'analyse chimique à $pH$ contrôlé : réactions chimiques spécifiques à un $pH$ bien précis (sang par exemple, piscine, aquarium...)
 
$-\ $ la formulation tamponnée de médicaments (aspirine...) et produits cosmétiques pour réduire les effets secondaires.
 
$-\ $ Les solutions tampons  ont surtout une très grande importance dans le domaine du monde vivant : la plupart des milieux biologiques sont des milieux de $pH$ pratiquement constant

Exemple : 

Le $pH$ du sang veineux humain se maintient à la valeur $pH=7.40$ grâce à la participation de plusieurs systèmes tampons parmi lesquels on peut citer le couple $H_{2}PO_{4}^{2-}|HPO_{4}^{2-}$ de $pK_{a}=7.2$

4. Compléments 

4.1 $pH$ et biologie

Les fonctions organiques de l'être humain obéissent à des constantes biologiques soit acides, soit basiques. 
 
Ainsi le cerveau et le liquide céphalo-rachidien sont alcalins, leur $pH$ varie entre $7.9$ et $8.1.$
 
La bouche et la salive sont naturellement alcalines : $pH$ de $7.1$ à $7.4.$
 
La salive contient des bicarbonates qui sont chargés de neutraliser les toxines alimentaires acides et l'acide lactique issus du sucre et autres glucides). 
 
Le sang est également alcalin, son $pH$ normal, à la température du corps, varie entre $7.38$ et $7.43.$
 
Le $pH$ de l'humeur aqueuse et celui de la lymphe sont voisins de $7.9.$
 
Le $pH$ de l'oreille interne se tient aux alentours de $7.4.$
 
Les diverses sécrétions (mucus, glaire, bile, larmes, sécrétions utérines, sperme) sont généralement tamponnées pour maintenir la réaction du milieu dans une zone favorable à l'activité des enzymes (diastases).
 
Les selles normales sont très légèrement alcalines $(pH$ entre $7.0$ et $7.5)$ : un $pH$ de $6$ est donc signe de fermentations anormales.
 
En revanche, les sécrétions de l'estomac sont très acides : le suc gastrique contient de l'acide chlorhydrique libre et son $pH$ est voisin de $1$ (chez l'adulte). 
 
Les sécrétions vaginales sont acides par la présence d'acide lactique : leur $pH$ est de $4.5.$
 
Le $pH$ normal de l'urine est acide et varie entre $5.8$ et $6.2.$ 
 
Les acides biliaires ont un $pH$ qui varie entre $3.8$ et $4.3.$
 
Tous ces $pH$ biologiques correspondent à l'état normal. 
 
Des variations entraînent des troubles pathologiques (stress, maladies...)
 
Les phénomènes vitaux ne peuvent se produire que dans une zone très limitée de $pH$, en dehors de laquelle toute vie, depuis celle du plus simple des microorganismes jusqu'à celle de l'homme, peut être paralysée. 
 
Une telle sensibilité aux variations du $pH$ nécessite une possibilité de régulation très efficace : les milieux biologiques sont tamponnés, et souvent alcalins.
 
Ainsi, l'eau des mers dont on pense aujourd'hui qu'elle fut la soupe prébiotique, d'où les premières formes vivantes émergèrent et des océans constitue un énorme milieu tamponné : la vie n'y est possible que si le $pH$ varie en moyenne entre $7.5$ et $8.0.$
 
Une acidification du $pH$ marin (fonte des glaces, pluies acides, chaleur excessive) entraîne les migrations saisonnières de certains poissons qui ne peuvent se développer en milieu trop acide. 
 
Chez les animaux supérieurs et chez l'homme, c'est le $pH$ du milieu intérieur qui reste constant : le $pH$ du contenu cellulaire varie peu, tout comme celui du milieu extracellulaire.

4.2 La demi-équivalence

4.2.1 Définition

A la demi-équivalence $[\text{Acide faible}]_{1/2E}=[\text{base faible}]_{1/2E}$ : 
 
D'où  $pH_{1/2E}=pKA.$
 
Un mélange qui contient en égales quantités les deux partenaires d'un couple acide-base est appelé solution tampon.

4.2.2 Solution tampon

Les propriétés d'une solution tampon constituent l'effet tampon :
 
$-\ $ ne varie pratiquement pas par addition d'un acide en quantité modérée, le $pH$ de la solution 
 
$-\ $ ne varie pratiquement pas par addition d'une base en quantité modérée,
 
$-\ $ ne varie pratiquement pas par addition d'eau même en quantité importante.
 
L'effet tampon est d'autant plus marqué que :
 
$-\ $ les concentrations $[A]$ et $[B]$ sont plus voisines,
 
$-\ $ les concentrations $[A]$ et $[B]$ sont plus grandes

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Notion d'acide fort et de base forte : Réaction entre acide fort et base forte - Ts

Classe: 
Terminale
 

I. Acide fort

1. Étude d'un exemple : le chlorure d'hydrogène

1.1 Étude qualitative

Le chlorure d'hydrogène $HCl$, à la température ordinaire, est un gaz très soluble dans l'eau.
 
Les solutions obtenues par mise en solution du chlorure d'hydrogène dans l'eau portent le nom de solutions d'acide chlorhydrique
 
Une solution d'acide chlorhydrique conduit le courant électrique et subit l'électrolyse ; elle contient donc des porteurs de charge c'est-à-dire des  ions
 
La présence des ions $Cl^{-}$ se caractérise par la formation d'un précipité blanc de chlorure d'argent $AgCl$ quand on ajoute quelques gouttes d'une solution de nitrate d'argent
 
La mise en évidence d'ions hydroduim $H_{3}O^{+}$ s'effectue au moyen d'un indicateur coloré : l'hélianthine
 
Quand on verse quelques gouttes d'acide chlorhydrique dans de l'eau distillée additionnée de quelques gouttes d'hélianthine, une couleur rouge apparait 
 
Les solutions d'acide chlorhydrique sont très corrosives ; la dilution des solutions concentrées est très exothermique et s'accompagner de projections.  

1.2 Étude quantitative

A partir d'une solution commerciale de chlorure hydrogène, on réalise, par dilution, une solution de concentration $C=10^{-2}mol\cdot L^{-1}$
 
La mesure du $pH$ de la solution diluée à l'aide d'un $pH-$ mètre donne la valeur égale $2$
 
Montrons que l'acide chlorhydrique est un acide fort
 
Les espèces chimiques présentes dans la solution :
 
$-\ $ les ions hydronium $H_{3}O^{+}$ provenant de l'autoprotolyse de l'eau et du chlorure d'hydrogène $HCl$
 
$-\ $ des ions $Cl^{-}$ provenant de l'action de l'eau sur le chlorure d'hydrogène
 
$-\ $ des ions $OH^{-}$ provenant de l'autoprotolyse de l'eau
 
$-\ $ et éventuellement des molécules de chlorure d'hydrogène $HCl$ non ionisées 
 
$pH=2\Rightarrow\left[H_{3}O^{+}\right]=10^{-2}mol\cdot L^{-1}$
 
Le produit ionique s'écrit :
 
$\begin{array}{lcl} Ke&=&\left[H_{3}O^{+}\right]\left[OH^{-}\right]\\&\Rightarrow&\left[OH^{-}\right]=\dfrac{Ke}{\left[H_{3}O^{+}\right]}\\&=&\dfrac{10^{-14}}{10^{-2}}\\&\Rightarrow&\left[OH^{-}\right]=10^{-12}mol\cdot L^{-1} \end{array}$
 
L'électroneutralité de la solution s'écrit :
 
$\begin{array}{lcl} \left[H_{3}O^{+}\right]&=&\left[OH^{-}\right]+\left[Cl^{-}\right]\\&\Rightarrow&\left[Cl^{-}\right]=\left[H_{3}O^{+}\right]-\left[OH^{-}\right]\\&=&10^{-2}-10^{-12}\\&\Rightarrow&\left[Cl^{-}\right]=10^{-2}mol\cdot L^{-1} \end{array}$
 
La conservation de la matière s'écrit :
 
$\begin{array}{lcl} \left[HCl\right]_{i}&=&\left[HCl\right]_{d}+\left[HCl\right]_{r}\\&\Rightarrow&\left[HCl\right]_{r}=\left[HCl\right]_{i}-\left[HCl\right]_{d}\\&=&C-\left[Cl^{-}\right]\\&=&10^{-2}-10^{-2}\\&\Rightarrow&\left[HCl\right]_{r}=0\,mol\cdot L^{-1} \end{array}$
 
Les molécules de chlorure d'hydrogène $HCl$ n'existent pratiquement pas en solution 
 
La réaction entre le chlorure d'hydrogène $HCl$ et l'eau est donc totale et l'on écrit :
$$HCl\ +\ H_{2}O\ \rightarrow\ H_{3}O^{+}\ +\ Cl^{-}$$
 
La réaction entre le chlorure d'hydrogène $HCl$ et l'eau étant totale, on dit que $HCl$ est un acide fort

2. Solutions aqueuses d'acides forts

2.1 Définition

Un acide fort est une espèce chimique qui s'ionise totalement dans l'eau pour donner des ions hydronium $H_{3}O^{+}$

2.2 Exemples d'acides forts

$HCl$ : acide chlorhydrique ;
 
$HBr$ : acide bromhydrique ;
 
$HI$ : acide iodhydrique ;
 
$HNO_{3}$ : acide nitrique ;
 
$HClO_{4}$ : acide perchlorique ;
 
$H_{2}SO_{4}$ : acide sulfurique (diacide)

2.3 $pH$ d'une solution d'acide fort

Soit une solution aqueuse de monoacide fort $AH$ de concentration molaire $C$
 
L'action de l'eau sur l'acide est une réaction totale qui se traduit par l'équation-bilan : 
$$AH\ +\ H_{2}O\ \rightarrow\ H_{3}O^{+}\ +\ A^{-}$$
 
$\left[H_{3}O^{+}\right]=pH$
 
$\Rightarrow pH=-\log\left[H_{3}O^{+}\right]$
 
$\Rightarrow pH=-\log\,C$
 
Pour une solution d'un diacide fort, l'équation-bilan s'écrit :
$$AH_{2}\ +\ 2H_{2}O\ \rightarrow \ 2H_{3}O^{+}\ +\ A^{2-}$$
 
$\left[H_{3}O^{+}\right]=2C$
 
$\Rightarrow pH=-\log\left[H_{3}O^{+}\right]$
 
$\Rightarrow pH=-\log\,2C$

Remarque :

Pour des concentrations molaires volumiques $C$ telles que $10^{-6}mol\cdot L^{-1}<C<10^{-1}mol\cdot L^{-1}$, c'est la réaction :
 
$AH\ +\ H_{2}O\ \rightarrow \ H_{3}O^{+}\ +\ A^{-}$ qui est prépondérante
 
Pour des concentrations $C>10^{-6}mol\cdot L^{-1}$, c'est la réaction d'autoprotolyse de l'eau $\left(2H_{2}O\ \rightarrow\ H_{3}O^{+}\ +\ OH^{-}\right)$ qui est prépondérante
 
Quand on dilue à l'infini une solution acide le $pH$ tend vers $7$

II. Base forte

1. Étude d'un exemple : l'hydroxyde de sodium $NaOH$

1.1 Étude qualitative

L'hydroxyde de sodium ou soude est un solide blanc de formule $NaOH.$
 
C'est un solide ionique, constitué d'ions sodium $Na^{+}$ et d'ions hydroxyde $OH^{-}$ dont la mise en solution est fortement exothermique
 
La présence des ions sodium $Na^{+}$ est mise en évidence par le test à la flamme.
 
La couleur jaune orange de la flamme révèle la présence de l'élément sodium
 
La mise en évidence des ions $OH^{-}$ s'effectue au moyen d'un indicateur coloré : la phénolphtaléine, une coloration rouge violacée apparait 
 
La couleur rouge violacé de la phénolphtaléine caractérise une solution contenant des ions hydroxyde $OH^{-}$
 
L'hydroxyde de sodium est un produit très corrosif.
 
Sa dissociation et la dilution de ses solutions concentrées sont très exothermiques et peuvent s'accompagner de projections

1.2 Étude quantitative 

On dissout $0.4\,g$ d'hydroxyde de sodium dans un $1\,L$ d'eau. 
 
La solution ainsi préparée a une concentration en $NaOH$ $C=10^{-2}mol\cdot L^{-1}$
 
La mesure du $pH$ de la solution à l'aide du $pH-$ mètre donne une valeur égale $12$
 
Montrons que la dissociation de l'hydroxyde de sodium $NaOH$ dans l'eau est totale
 
Les espèces chimiques présentes dans la solution sont : $Na^{+}$, $OH$, $H_{3}O^{+}$ et éventuellement $NaOH$ non dissociée 
 
$pH=12$
 
$\Rightarrow\left[H_{3}O^{+}\right]=10^{-12}$
 
$\Rightarrow\left[H_{3}O^{+}\right]=10^{-12}mol\cdot L^{-1}$
 
Le produit ionique de l'eau s'écrit :
 
$\begin{array}{lcl} Ke&=&\left[H_{3}O^{+}\right]\left[OH^{-}\right]\\&\Rightarrow&\left[OH^{-}\right]=\dfrac{Ke}{\left[H_{3}O^{+}\right]}\\&=&\dfrac{10^{-14}}{10^{-12}}\\&\Rightarrow&\left[OH^{-}\right]=10^{-2}mol\cdot L^{-1} \end{array}$
 
L'électroneutralité de la solution s'écrit :
 
$\begin{array}{lcl} \left[H_{3}O^{+}\right]+\left[Na^{+}\right]&=&\left[OH^{-}\right]\\&\Rightarrow&\left[Na^{+}\right]=\left[OH^{-}\right]-\left[H_{3}O^{+}\right]\\&=&10^{-2}-10^{-12}\\&\Rightarrow&\left[Na^{+}\right]=10^{-2}mol\cdot L^{-1} \end{array}$
 
La conservation de la matière s'écrit :
 
$\begin{array}{lcl} \left[NaOHC\right]_{i}&=&\left[NaOHC\right]_{d}+\left[NaOHC\right]_{r}\\&\Rightarrow&\left[NaOHC\right]_{r}=\left[NaOHC\right]_{i}-\left[NaOHC\right]_{d}\\&=&C-\left[Cl^{-}\right]\\&=&\dfrac{0.4}{40\times 1}-10^{-2}\\&\Rightarrow&\left[NaOHC\right]_{r}=0\,mol\cdot L^{-1} \end{array}$
 
Les molécules d'hydroxyde de sodium $NaOH$ n'existent pratiquement pas en  solution 
 
La réaction entre l'hydroxyde de sodium $NaOH$ et l'eau est donc totale et l'on écrit :
$$NaOH\stackrel{H_{2}O}{\longrightarrow}\ Na^{+}\ +\ OH^{-}$$
 
La réaction entre l'hydroxyde de sodium $NaOH$ et l'eau étant totale, on dit que $NaOH$ est une base forte

2. Solutions aqueuses de bases fortes

2.1 Définition

Une base forte est une espèce chimique qui s'ionise totalement dans l'eau pour donner des ions hydroxyde $OH^{-}$ 

2.2 Exemples de bases fortes

$NaOH$ : hydroxyde de sodium ;
 
$KOH$ : hydroxyde de potassium ;
 
$Ca\left(OH\right)_{2}$ : hydroxyde de calcium (dibase) ;
 
$C_{2}H_{5}O^{-}$ : ion éthanoate
 
2.3 $pH$ d'une solution de base forte
 
Soit une solution aqueuse de monobase forte $BOH$ de concentration molaire  $C$
 
L'action de l'eau sur la base est une réaction totale qui se traduit par l'équation-bilan :
$$BOH\stackrel{H_{2}O}{\longrightarrow}\ OH^{-}\ +\ B^{+}$$
 
$\begin{array}{lcl} \left[OH^{-}\right]&=&C\\&\Rightarrow& pH=-\log\left[H_{3}O^{+}\right]\\&=&-\log\dfrac{Ke}{\left[OH^{-}\right]}\\&=&-\log\dfrac{10^{-14}}{C}\\&\Rightarrow&pH=14+\log\,C \end{array}$
 
Pour une solution d'une dibase forte, l'équation-bilan s'écrit :
$$B\left(OH\right)_{2}\stackrel{H_{2}O}{\longrightarrow}\ B^{2+}\ +\ 2OH^{-}$$
 
$\left[OH^{-}\right]=2C\ \Rightarrow\;pH=14+\log\,2C$

Remarque :

Pour des concentrations molaires volumiques $C$ telles que $10^{-6}mol\cdot L^{-1}<C<10^{-1}mol\cdot L^{-1}$, c'est la réaction :  
 
$BOH\stackrel{H_{2}O}{\longrightarrow}\ OH^{-}\ +\ B^{+}$ qui est prépondérante
 
Pour des concentrations $C<10^{-6}mol\cdot L^{-1}$, c'est la réaction d'autoprotolyse de l'eau 
            
$\left(2H_{2}O\right)\ \longrightarrow\ H_{3}O^{+}\ +OH^{-}$ qui est prépondérante
 
Quand on dilue à l'infini une solution basique le $pH$ tend vers $7$

III. Réaction entre acide fort et une base forte

1. Étude qualitative

Quand on mélange une solution d'acide chlorhydrique $HCl$ et un base $NaOH$, on constate :
 
$-\ $ une élévation de la température du milieu réactionnel : on dit que la réaction est exothermique 
 
$-\ $ une variation du $pH$ du milieu
 
$-\ $ une variation des quantités de matière des ions hydronium $H_{3}O^{+}$ et des ions hydroxyde $OH^{-}.$
 
Ce qui nous permet de conclure qu'il y a une réaction acide-base 
 
L'équation-bilan de la réaction s'écrit :
$$H_{3}O^{+}\ +\ OH^{-}\ \rightarrow\ 2H_{2}O$$
 
Cette réaction est la réaction inverse de l'autoprotolyse de l'eau ; elle est donc totale.
 
Les ions $Na^{+}$ et $Cl^{-}$ n'interviennent pas dans la réaction : ce sont des ions spectateurs

2. Étude quantitative 

2.1 Variation du $pH$ au cours de la réaction

2.1.1 Étude expérimentale

A l'aide d'une pipette jaugée, on place dans un bécher
 
Un volume $V_{A}$ d'acide chlorhydrique de concentration $C_{A}$ inconnue à déterminer
 
Puis à l'aide d'une burette graduée placée au-dessus du bécher, on verse petit à petit dans le bécher la solution d'hydroxyde de sodium de concentration $C_{B}$ connue (voir schéma du montage ci-dessous)
 
 
L'agitateur magnétique permet d'homogénéiser le mélange après ajout de la solution d'hydroxyde de sodium
 
Pour différentes valeurs de $V_{B}$ de soude ajouté, on mesure le $pH$ de la solution obtenue à l'aide $pH-$ mètre préalablement étalonné
 
On obtient la courbe $pH=f(V_{B})$ suivante :

2.1.2 Étude la courbe

La courbe $pH=f(V_{B})$ est croissante : elle présente deux parties distinctes
 
 
$-\ $ Pour $V_{B}\leq 8\,mL$, la courbe est presque rectiligne et le $pH$ varie peu lors de l'addition de la solution d'hydroxyde de sodium
 
$-\ $ Pour $8\,mL\leq V_{B}\leq 12\,mL$, nous observons un $«$ saut de $pH »$ et la courbe change de concavité
 
$-\ $ Pour $V_{B}\geq 12\,mL$, $pH$ varie peu
 
Ensuite faiblement, la courbe
 
Tendant vers une asymptote horizontale
 
Pour $V_{B}=9.8\,mL$, la courbe change de concavité : il existe donc un point d'inflexion dans cette partie de la courbe
 
Étudions les propriétés de la solution en ce point, noté $E$

2.2 Point d'équivalence

2.2.1 Définition

Il y a équivalence lorsque les réactifs ont été mélangés dans les proportions stœchiométriques de la réaction de dosage
 
La réaction étudiée ici a pour équation :
$$H_{3}O^{+}\ +\ OH^{-}\ \rightarrow\ 2H_{2}O$$
 
A l'équivalence :
 
$n_{H_{3}O^{+}}=n_{OH^{-}}\Rightarrow\ C_{A}V_{A}=C_{B}V_{BE}$

2.2.2 Détermination du point d'équivalence

Le point d'équivalence $E$ est le point de la courbe telque $V_{B}=V_{BE}$
  
Le point d'inflexion de la courbe correspond au point d'équivalence, ceci permet de déterminer la position de $E$ par la méthode des tangentes
 
$\bullet\ $ Méthode des tangentes
 
$-\ $ On trace tout d'abord deux tangentes à la courbe parallèles et situées de part et d'autre du point d'équivalent
 
$-\ $ On trace une parallèle à ces deux tangentes équidistantes de celles-ci. 
 
Son intersection avec la courbe $pH=f(V_{B})$ détermine le point d'équivalent $E$
 
$\bullet\ $ Autre méthode : emploi des indicateurs colorés
 
Un indicateur coloré convient pour le dosage acido-basique si sa zone de virage contient le $pH$ du point d'équivalence $(pH_{E}=7)$
 
Le $B.B.T$ $($zone de virage : $6.1-7.6)$ est le plus approprié 
 
Mais étant donné l'amplitude de la variation du $pH$, l'hélianthine $(3.1-4.4)$ ou la phénolphtaléine convient également dès lors que les solutions intervenant dans le dosage ne sont très diluées

IV. Applications aux dosages

Les analyses constituent de nos jours une part importante de l'activité expérimentale des entreprises de chimie de synthèse, des organismes de contrôle ou des laboratoires de recherche : qu'elles soient bactériologiques, sanguines, d'urines, organiques ou minérales, les analyses reposent sur une technique appelée dosage. 
 
Mais les méthodes utilisées dépendent de la quantité et des propriétés de l'espèce à analyser, mais aussi de la précision souhaitée

1. Principe d'un dosage acido-basique 

Doser une espèce chimique dans une solution consiste à déterminer la quantité de matière ou la concentration molaire inconnue de l'espèce en solution. 
 
Pour cela, on réalise une réaction acidobasique qui doit impérativement être :
 
$\bullet\ $ unique : l'espèce titrante ne doit pas réagir avec d'autres espèces que l'espèce à titrer, et ne doit pas donner d'autres produits que ceux de la réaction de titrage, sinon la mesure du volume versé n'est pas fiable
 
$\bullet\ $ totale : chaque goutte de l'espèce titrante doit réagir intégralement avec l'espèce à titrer, sinon la mesure du volume versé n'est pas fiable
 
$\bullet\ $ et rapide : on ne doit pas être obligé d'attendre plusieurs minutes ou plusieurs heures après chaque ajout de l'espèce titrante
 
La relation entre les concentrations des solutions acide et basique à l'équivalence permet de calculer la concentration inconnue.
 
Il existe deux moyens pour déterminer l'équivalence : le dosage colorimétrique et le dosage $pH-$ métrique

2. Dosage $pH-$ métrique

 
Pour doser une solution acide, par exemple, on utilise le montage ci-dessus.
 
On place cette solution dans le bécher $($volume $V_{A}$ connu ; concentration $C_{A}$ à déterminer$)$ en ajoutant, si nécessaire, de l'eau distillée, pour que les électrodes trempent correctement $($cet ajout ne modifie pas la quantité d'ions $H_{3}O^{+})$ et la solution d'hydroxyde de sodium $($concentration $C_{B}$ connue$)$ dans la burette graduée. 
 
On note les valeurs de $pH$ correspondant à l'ajout du volume $V_{B}$ de solution d'hydroxyde de sodium
 
On trace la courbe représentant $pH=f(V_{B})$ sur papier millimétré, on détermine le point d'équivalence $E$ soit en considérant qu'il correspond à $pH=7$, soit en utilisant la méthode des tangentes parallèles et on calcule la concentration

3. Dosage colorimétrique

Les indicateurs colorés sont des substances dont la couleur dépend du $pH$ ; leur changement de couleur se produit dans un domaine de $pH$ relativement étroit que l'on appelle zone de virage
 
Tableau présentant les trois principaux indicateurs colorés usuels avec leur zone de virage
$$\begin{array}{|c|c|c|c|} \hline \text{Indicateur coloré}&\text{Couleur acide}&\text{zone de virage}&\text{Couleur basique}\\ \hline \text{Hélianthine}&\text{rouge}&3.1-4.4&\text{jaune}\\ \hline \text{Bleu de bromothymol}&\text{jaune}&6.0-7.6&\text{bleu}\\ \hline \text{Phénolphtaléine}&\text{incolore}&8.2-10.0&\text{rose}\\ \hline \end{array}$$
 
Dans un dosage colorimétrique, il faut choisir un indicateur coloré dont la zone de virage contient le $pH$ du point d'équivalence.
 
Dans le cas d'un dosage acide fort - base forte, le $pH$ du point d'équivalence est égal à $7.0$ et le bleu de bromothymol $($zone de virage $6.0-7.6)$ est un indicateur qui convient dans tous les cas, que les solutions soient concentrées ou diluées

4. Application : dosage d'une base forte par un acide fort

 
La courbe $pH$ en fonction de $V_{B}$ est décroissante : elle comporte trois parties distinctes :
 
$-\ $ pour $V_{a}\leq 8\,mL$, la courbe est presque rectiligne et le $pH$ varie peu lors de l'addition de l'acide fort
 
$-\ $ pour $8\,mL\leq V_{a}\leq 12\,mL$, on observe un $«$ saut de $pH$ $»$ et la courbe change de concavité-pour $V_{a}\geq 12\,mL$, le $pH$ varie ensuite faiblement, la courbe tendant vers une asymptote horizontale
 
Dans cette zone ou la concavité de la courbe s'inverse, le $pH$ varie beaucoup et on y trouve le point équivalent $E.$
 
La connaissance de $E$ va permettre de calculer la concentration $C_{a}$ inconnue

Exercice d'application

D'après le graphe représentant la variation du $pH$ en fonction du volume d'acide versé :
 
Il faut verser $8.5\,mL$ d'une solution d'acide chlorhydrique de concentration molaire $10^{-2}mol\cdot L^{-1}$ dans $20\,mL$ d'une solution d'hydroxyde de sodium pour obtenir l'équivalence acido-basique.
 
1) Quel est le $pH$ à l'équivalence ?
 
2) Calculer la concentration molaire de la solution basique.
 
Quel est le $pH$ de la solution basique ?
 
3) Vers quelle valeur tend le $pH$ de la solution lorsqu'on continue à ajouter la solution acide ?
 
4) En utilisant les résultats précédents, tracer le graphe représentant la variation du $pH.$
 
5) Calculer la concentration molaire des ions spectateurs $Na^{+}$ et $Cl^{-}$ présents dans le bécher à l'équivalence... ainsi que celles des ions $H_{3}O^{+}$ et $OH^{-}.$
 
En déduire la masse de chlorure de sodium $NaCl$ dissoute à l'équivalence.
 
Cette masse augmente-t-elle après l'équivalence ?

Solution 

1) Le $pH$ à l'équivalence est égale $7$
 
2) Calcul de la concentration molaire de la solution basique
 
A l'équivalence : 
 
$\begin{array}{lcl} C_{B}V_{B}&=&C_{A}V_{A}\\&\Rightarrow&C_{B}=\dfrac{C_{A}V_{A}}{V_{B}}\\&=&\dfrac{1\cdot 10^{-2}\times 8.5}{20}\\&\Rightarrow&C_{B}=4.25\cdot 10^{-3}mol\cdot L^{-1} \end{array}$
 
3) Valeur vers laquelle tend le $pH$ de la solution lorsqu'on continue à ajouter la solution acide 
 
Lorsqu'on continue à ajouter la solution acide $n_{A}>n_{B}$ ; la solution est donc acide
 
$\Rightarrow\ pH=-\log\,C_{A}\text{ avec }C_{A}=\dfrac{C_{A}V_{A}}{V_{A}+V_{B}}$
 
$\Rightarrow\ pH=-\log\dfrac{C_{A}V_{A}}{V_{A}+V_{B}}=-\log\dfrac{V_{A}C_{A}}{V_{A}\left(1+\dfrac{V_{B}}{V_{A}}\right)}$
 
$\Rightarrow\ pH=-\log\,C_{A}\text{ car }\dfrac{V_{B}}{V_{A}}\rightarrow\;0$
 
$\Rightarrow\ pH=-\log\;1\cdot 10^{-2}\ \Rightarrow\;pH=2$
 
4) Tracé du graphe représentant la variation du $pH$
 
 
5) Calcul de la concentration molaire des ions spectateurs $Na^{+}$ et $Cl^{-}$ et des ions $H_{3}O^{+}$ et $OH^{-}$ à l'équivalence
 
$\begin{array}{lcl} \left[Cl^{-}\right]&=&\dfrac{C_{A}V_{A}}{V_{A}+V_{B}}\\&=&\dfrac{1\cdot 10^{-2}\times 8.5}{8.5+20}\\&\Rightarrow&\left[Cl^{-}\right]=2.98\cdot 10^{-3}mol\cdot L^{-1} \end{array}$
 
$\begin{array}{lcl} \left[Na^{+}\right]&=&\dfrac{C_{B}V_{B}}{V_{A}+V_{B}}\\&=&\dfrac{4.25\cdot 10^{-3}\times 20}{8.5+20}\\&\Rightarrow&\left[Na^{+}\right]=1.49\cdot 10^{-4}mol\cdot L^{-1} \end{array}$
 
$\left[H_{3}O^{+}\right]=10^{-7}mol\cdot L^{-1}$
 
$\left[OH^{-}\right]=10^{-7}mol\cdot L^{-1}$
 
Masse de chlorure de sodium $NaCl$ dissoute à l'équivalence.
 
$\begin{array}{lcl} m_{NaCl}&=&n_{NaCl}\times M_{NaCl}\\&=&C_{A}V_{A}\times M_{NaCl}\\&=&1\cdot 10^{-2}\times 8.5\cdot 10^{-3}\times(23+35.5)\\&\Rightarrow&m_{NaCl}=4.97\,mg \end{array}$
 
Cette masse n'augmente pas après l'équivalence car elle dépend de la quantité d'hydroxyde de sodium dosée   
 
Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Pages