Réactions chimiques Équation - bilan - 2nd S
I. Exemples de réactions chimiques
1. Réaction entre le fer et le soufre
1.1 Expérience

1.1.1 Observations
1.1.2 Interprétation
1.2 Conclusion
2. Réaction entre le fer et le dioxygène
2.1 Expérience



Exercice 1
Les énergies des différents niveaux, exprimés en électron-volt, sont données par la formule :
$E_{n}=\frac{13,6}{n^{2}}1$.Calculer les énergies correspondant à $n = 1, 2, 3$ et $\infty$ et représenter le diagramme
des niveaux d'énergie de l'atome d'hydrogène.
2. Quelle est l‟énergie minimale que l'on doit fournir à un atome d'hydrogène pour qu'il
passe de l'état fondamental à un état excité ? La transcrire sur le diagramme.
3. Cette énergie est apportée à l'atome par une radiation lumineuse monochromatique.
Calculer sa longueur d'onde.
4. Calculer la longueur d‟onde de la radiation susceptible d'ioniser l'atome d'hydrogène
Exercice 2
1 Rutherford a décrit l'atome d'hydrogène par le modèle planétaire : l'électron a un
mouvement circulaire, de rayon $r$, autour d‟un noyau constitué de proton.
La force électrique subie l‟électron est dirigée selon la droite proton-électron, attractive de
valeur $F={Ke^{2}}{r^{2}}$
La force gravitationnelle est négligeable devant cette force
a) Montrer que le mouvement de l'électron est uniforme
b) Etablir l'expression de la vitesse v en fonction de $k, e, r$ et $m$
c) Exprimer son énergie cinétique en fonction de ces mêmes paramètres.
d) Exprimer en énergie mécanique E en fonction de $k$, e et r sachant que son énergie
potentielle est : $E_{p}=\frac{ke^{2}}{r}$
Quelle est sa limite quand $r$ tend vers l'infini
2. Différents faits expérimentaux ontconduit Niels Bohr à formuler l'hypothèse suivante :
l'électron ne se déplacer que sur certains cercles dont les rayons $r_{n}$ obéissent à la loi :
$v_{n}r_{n}=\frac{nK}{m}$ ;
$K$ constante universelle :$ K= 1,054.10^{34}. K J s n$ : nombre entier $n\geq{1} ; v_{n}$ vitesse
de l'électron sur le cercle de rayon $ r_{n}$
a)Déterminer l'expression de $r_{n}$ en fonction des constantes $k, K, m, e$ et $n$. Exprimer $r_{n}$ en
fonction de $ r_{1}$ . Calculer $ r_{1}$
b) Déterminer l'expression de $E_{n}$ , énergie mécanique de l'électron sur le cercle de rayon $r_{n}$
, en fonction des mêmes paramètres Exprimer $E_{n}$ en fonction de $ E_{1}$
c) Calculer $ E_{1}$ et $ E_{2}$ en électronvolts. Quelle cause peut faire passer l'énergie de l'électron
de $ E_{1}$ à $ E_{2}$ . $m_{e} = 9,109.10^{-31}Kg ; e =1,602.10^{-19} ; k = 9,000.10^{9}SI$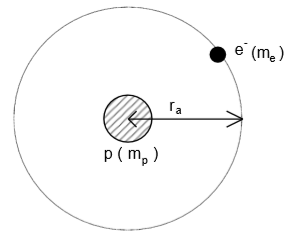
Exercice3 L’atomed’hydrogène
Diagramme d'énergie de l'atome d'hydrogène obtenu à partir de la formule : $E_{n} =\frac{13,6}{n^{2}} (en eV)$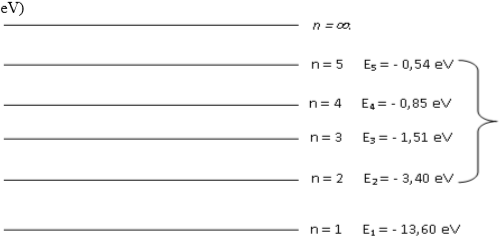
1) Quel est le nom du nombre noté $"n"$ qui apparaît dans le diagramme ?
2) Quand dit-on qu'un atome est dans son état fondamental ? Quel est l'état fondamental de
l'atome d'hydrogène ? Le noter sur le schéma.
3) Considérons une population d'atomes d'hydrogène au repos, sans apport d'énergie de la part de l'extérieur.
Dans quel état se trouvent les atomes (ou du moins l‟immense majorité) ?
4) Que représente le niveau noté : $n = ∞$ ? Noter son nom sur le schéma.
5) Quelle énergie minimale, en $eV$, faut-il fournir à un atome d'hydrogène pour l'ioniser
lorsqu'il est dans son état fondamental ?
6) Un atome d‟hydrogène a la configuration électronique telle que : $n = 3$
.Est-il dans son état fondamental ? Comment s'appelle un tel état ?
.Le représenter par un petit point sur le diagramme précédent.
7) L'atome d'hydrogène peut-il se trouver dans un état situé entre les niveaux $n = 1$ et $n = 2$ ?
8) L'atome d'hydrogène est excité sur le niveau : $n = 3$.
.Comment peut-on exciter cet atome ?
.Montrer qu'en se désexcitant vers le niveau $2$, il émet un photon de longueur d'onde : $\lambda= 656,1 nm$.
Cette radiation est-elle située dans les $X$, les $UV$, le visible ou l'IR ?
.Représenter par une flèche, sur le diagramme précédent, la transition correspondant à cette désexcitation.
9) Une radiation émise par l'atome d'hydrogène a une énergie égale à : $E = 2,54 eV$
Cette radiation émise par l'atome d'hydrogène fait partie de la série de Balmer (retour au niveau $n = 2$).
Déterminer la transition électronique correspondant à l'émission de cette
radiation. La noter sur le schéma.
. Calculer la longueur d'onde correspondante.
10) Une lampe à décharge à hydrogène émet-elle un spectre continu de radiations ou un spectre discontinu ?
Exercice 4
Données : célérité de la lumière dans le vide :$3 108 m/s$; constante de Planck : $h=6,62 10-34 Js$ ;
charge élémentaire : $e = 1,6 10^{-19} C$ ; masse de l'électron $m = 9 10^{-31} kg$.
La figure représente un diagramme très simplifié des niveaux
d'énergie de l'atome de lithium de numéro atomique $Z=3$, de formule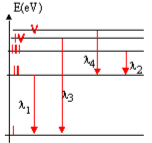
électronique $K^{2}L^{1}$.
On considère les quatre transitions représentées sur le diagramme.
Les longueurs d'ondes correspondantes sont $λ_{1} = 671 nm ; λ_{2} = 812
nm ; λ_{3} = 323 nm$ et $λ_{4} = 610 nm$.
1. Expliquer brièvement niveau d'énergie et spectres de raies.
2. Montrer qu'entre l'énergie $E(en eV)$ d'un photon et sa longueur
d'onde $λ$ il existe la relation $E= 1240 /λ. λ$ étant exprimé en $nm$ et $E$ en $eV$.
- Déterminer l'énergie $(eV)$ des photons émis lors de chacune des $4$ transitions.
3. L'énergie du niveau $I$ vaut $E_{1} = - 5,39 eV$. C'est l'énergie de l'électron externe dans son état
fondamental. Affecter l'énergie $E_{i} (eV)$ à chaque niveau du diagramme.
Pour quelle valeur de la longueur d'onde des radiations incidentes les atomes de lithium
subiront-ils une ionisation à partir de l'état fondamental ?
Exercice5 : Niveaux d’énergie de l’atome d’hydrogène
On s'intéresse dans ce qui suit aux niveaux d'énergie des atomes d'hydrogène et de sodium,
tous deux éléments de la première colonne du tableau de classification périodique.
1/ Les niveaux d'énergie de l'atome d'hydrogène sont donnés par la relation :$E_{n}=-13,6/n²$ où
En en $eV$ et $n$ un entier naturel non nul.
1-1 Déterminer l‟énergie minimale en $eV$, qu'il faut fournir à l'atome d'hydrogène pour
l'ioniser dans les cas suivants :
 1-1.2 L'atome d'hydrogène est à l'état excité correspondant au niveau d'énergie $(n = 2)$.
1-1.2 L'atome d'hydrogène est à l'état excité correspondant au niveau d'énergie $(n = 2)$.
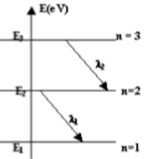
2/ On donne ci-après le diagramme simplifié des niveaux d'énergie de l'a tome de sodium
(l'échelle n‟est pas respectée).
L'état fondamental correspond au niveau d'énergie $E_{1}$. Les niveaux d'énergie $E_{2}$ et $E_{3}$
correspondant à des états excités.
2-1 Lorsque l'atome passe de $E_{2}$ à $E_{1}$ il émet une radiation de longueur d'onde $λ_{1}=589 nm$;
lorsqu'il passe de $E_{3}$ à $E_{2}$, il émet une radiation de longueur d'onde $λ_{2}=568,8nm$.
En expliquant le raisonnement, calculer la différence d‟énergie $(E_{3}-E_{1})$ en $eV$.
2-2 Lorsque l'atome, initialement dans son état fondamental, est éclairé par un faisceau
monochromatique de longueur d'onde $λ$ convenable, il peut directement passer du niveau
d'énergie $E_{1}$ au niveau d‟énergie $E_{3}$.
Exprimer la longueur d'‟onde $λ$ de ce faisceau en fonction des longueurs d'onde $λ_{1}$ et $λ_{2}$.
Faire l'application numérique
Exercice 6
La mécanique quantique montre que l'état fondamental de l'atome d'hydrogène est caractérisé
par une énergie $E_{1} =-13,6ev$ et chaque niveau excité $n >1$ est définie par une énergie
$E_{n}=\frac{E_{0}}{n^{2}} (n$ est un entier naturel positif) avec $E_{0} = 13,6ev$.
1-/A quoi correspond l'énergie $E_{0}$ ?
2-/ Quelle relation simple existe entre l'énergie de transition$ \Delta{E}$ d'un niveau $n$ à un niveau $p$ et
la longueur d'onde du photon émis ou absorbé. (Traiter chaque cas à part)
3-/a-/ Montrer que pour une transition d'un niveau $p$ à un niveau $n$ tel que $p > n$, on peut écrire
la relation $\frac{1}{\lambda}=R_{H}(\frac{1}{n^{2}}-\frac{1}{P^{2}})$.
b-/ Vérifier que RH (appelée constante de Rydberg) vaut $RH = 1,10.10^{+7}m^{-1}$
c--/Dans la série de Balmer (le retour au niveau $n = 2$) l'atome $H$ émet $1$ spectre contenant $4$
raies visibles, on se propose de calculer deux longueurs d'ondes de $2$ raies de ce spectre
correspondant à $p=3 ( \lambda{3,2})$ et $p =4 ( \lambda{4,2})$. Sans faire de calcul, et en utilisant $\lambda{E}$, comparer
$\lambda{3,2}$ et $\lambda{4,2}$ puis calculer leurs valeurs.
4-/ L'atome $H$ est dans son état fondamental $(n=1)$, on l'excite à l'aide d'un photon incident
d'énergie $W=13,8 e$v. Que se passe-t-il ? Calculer ( en $ev$) l'énergie cinétique $Ec$ de l'électron de
$H$ éjecté.
5/ si l'atome entre en choc inélastique avec un électron ayant une énergie cinétique égale
$11 ev$, que se passe-t-il ?
Exercice7
|
Données : charge élémentaire : $e = 1,6.10^{-19} C$ Constante de Planck : $h = 6,62.10^{-34} J.s$ célérité de la lumière dans le vide : $c = 3.10^{8} m.s^{-1} 1eV = 1,6.10^{-19} J 1nm = 10^{-9} m$ |
Le spectre de l'atome d‟hydrogène est obtenu par décharge électrique dans un tube contenant
du dihydrogène sous faible pression. Deux électrodes situées à chaque extrémité du tube
permettent d'appliquer une différence de potentiel.
Lorsque les paramètres ($d.d.p$, température, pression) sont correctement fixés, on observe
l'émission de lumière dont l'analyse est faite à l'aide d'un spectroscope.
Le spectre obtenu est constitué, dans sa partie visible, de quatre raies notées $ H_{\alpha} H_{\beta}H_{\gamma}H_{\delta}$
de longueurs d'onde respectives dans le vide : $656,27 nm ; 486,13 nm ; 434,05 nm ; 410,17 nm$.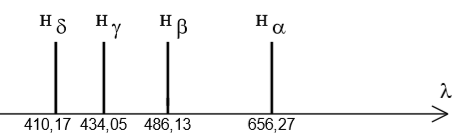
Spectre d'émission de l'atome d'hydrogène
1. Sachant que les couleurs des raies émises sont bleue, indigo, rouge et violette, restituer à
chaqueradiationsa couleur.
2. En $1885$, le physicien suisse Balmer, remarque que les longueurs d'onde $\lambda$ de ces quatre
radiations satisfont à une relation empirique :
| $\lambda=\lambda_{0}\frac{n^{2}}{n^{2}-4}$ |
$\lambda_{0} = 367,7 nm,n$ est un nombre entier naturel non nul ($n\ne{N*}$)
2.1. Indiquer la plus petite valeur possible de $n$. En déduire la longueur d'onde de la raie correspondante.
2.2. Quelles valeurs doit prendre $n$ pour retrouver les autres raies visibles du spectre ?
3. Les niveaux d'énergie quantifiés de l'atome d'hydrogène sont donnés par la relation :
$E_{n}=-\frac{E^{0}}{n^{2}}(eV)$
Pour $n = 1$ l'énergie de l'atome est minimale, l'atome est dans son état fondamental.
Pour toutes les autres valeurs de $n (n\geq{2} )$, l'atome est dans un état excité.
3.1. Expliquer brièvement le terme “ niveau d'énergie quantifié ”.
Que représente $E_{0}$ pour l'atome d'hydrogène ?
3.2. Etablir, en fonction de $n$, la fréquence $2 ,V_{n,2}$ (exprimée en $Hz$) des radiations émises
lorsque cet atome passe d'un état excité $n> 2$ à l'état excité $n = 2$.
3.3. Retrouver l'expression empirique de Balmer : $\lambda=\lambda_{0}\frac{n^{2}}{n^{2}-4},
\lambda$ étant exprimée en $nm$.
$A$ quelle transition correspond l'émission de la radiation de longueur d'onde $\lambda_{0}$ ? Justifier la
réponse.
3.4. Tracer le diagramme représentant les transitions entre les différents niveaux d'énergie de
l'atome d'hydrogène pour les quatre raies $ H_{\alpha} ,H_{\beta},H_{\gamma},H_{\delta}$de la série de Balmer.
4.1. Quelle est l'énergie cinétique minimale d'un électron projectile capable de provoquer par
choc l'excitation d'un atome d'hydrogène de son état fondamental à son deuxième état excité ?
4.2. Sous quelle tension minimale cet électron projectile, initialement au repos, a-t-il été accéléré ?
4.3. L'atome d'hydrogène précédemment excité revient à son état fondamental avec émission de deux photons.
Déterminer les longueurs d'onde de ces deux photons.
Exercice 8 :Données :$h = 6,62\times{10^{-34}} J.s ; c = 3,00\times{10^{8}} m.s^{-1}$ et $e = 1,60\times{10^{-19}}C$
Les lampes à vapeur de lithium contiennent de la vapeur de lithium à très faible pression.
Cette vapeur est excitée par un faisceau d‟électrons qui traverse le tube. Les atomes de lithium
absorbent l'énergie des électrons. L'énergie est restituée lors du retour à l'état fondamental
sous forme de radiations lumineuses.
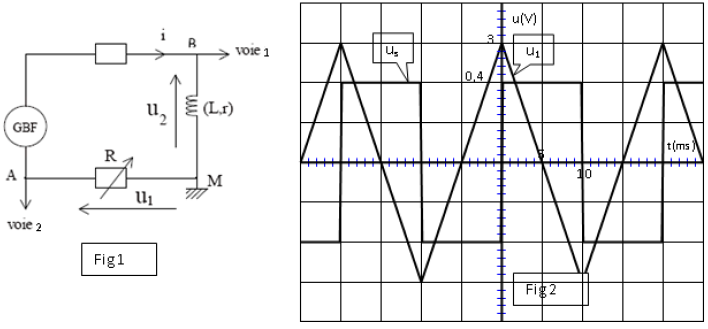
On représente le diagramme des niveaux d'énergie de l'atome de lithium (figure 1) de
numéro atomique $Z=3$. L'analyse du spectre d'émission d'une lampe à vapeur de lithium
révèle la présence de raies de longueur d'onde $\lambda$ bien définie.
On donne le spectre d'émission et le spectre d'absorption de l'atome de lithium (figure 2).
1- Préciser le spectre d‟émission de l'atome de lithium et le spectre d‟absorption.
2- Représenter le schéma du montage qui permet d'obtenir le spectre d'émission.
3- A l'aide du spectre d'émission, interpréter la quantification de l'énergie de l'atome de lithium.
4- L'énergie du l'état fondamental vaut $E_{1} = -5.39 eV$. (C'est l'énergie de l'électron de la
couche externe dans son état fondamental).
a- Prélever les valeurs des longueurs d'onde $\lambda_{1} ; \lambda_{2}$ et $\lambda_{3}$.
b- Montrer que la longueur d'onde $\lambda$ du photon émis lors d'une transition du niveau $n$ au
niveau $p (n>p)$ est $\lambda= \frac{1241}{ En - Ep}$ avec $\lambda$ en $nm$ et $En – Ep$ en $ev$.
c- trouver les valeurs d'énergie des autres niveaux sachant que la longueur d'onde du photon
émis lors d'une transition du niveau :
.3 au niveau est égale à $812 nm$.
.4 au niveau est égale à $323 nm$.
5- définir l'énergie d'ionisation de l'atome de lithium. Donner sa valeur.
6- L'atome de sodium, considéré maintenant à l'état fondamental, reçoit une radiation
lumineuse dont le quantum d'énergie a une longueur d‟onde $\lambda$ égale à :
a- $220 nm$.
$b- 300nm$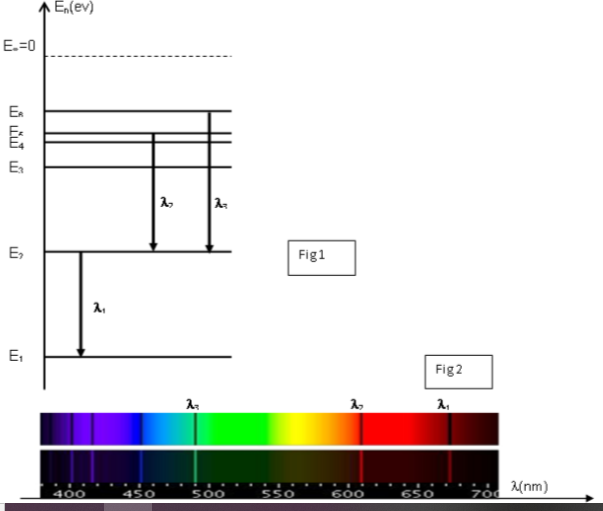
Exercice 9
Dans le spectre d'émission de l'atome d'hydrogène on trouve
les quatre raies suivantes, caractérisées par leur longueur
d'onde :
$\lambda_{1}=410 nm$ (violet),$ \lambda_{2}=434,1 nm$ (indigo),$ \lambda_{3}=486,1 nm$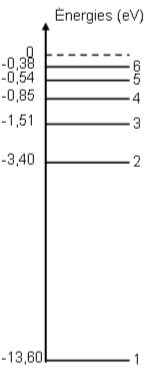
(bleu) et$ \lambda_{4}=656,3 nm$ (rouge). On donne le diagramme des
niveaux d'énergie de l'atome d'hydrogène.
1) Justifier la discontinuité du spectre d‟émission.
a- Que signifie l'état fondamental de l'atome ?
b-Définir l'énergie d'ionisation de l'atome d'hydrogène.
Donner sa valeur.
2) a-Calculer la longueur d'onde maximale $\lambda_{max}$
correspondant à la transition de l'électron d‟un niveau $n>2$
au niveau $2$. Déduire que $\lambda_{max} = \lambda_{4}$.
b-A quelle transition correspond chacune des radiations de
longueur d'onde $\lambda_{1}, \lambda_{2}$ et $\lambda_{3}$.
3) a- L'atome 'hydrogène est dans son niveau d'énergie$ E_{2}
(n=2)$, reçoit un photon incident de longueur d‟onde $\lambda=486.1
nm$. Ce photon est-il absorbé ? justifier sans calcul.
b-L'atome d'hydrogène est dans son état fondamental, reçoit :
. Un photon d‟énergie $11 ev$.
. Un électron incident d'énergie cinétique $11 ev$.
. Un photon d‟énergie $14,3 ev$.
Dire, en le justifiant ce qui se passe dans chaque cas (dans le cas où l'atome est ionisé donner
l'énergie cinétique de l'électron émis).
Exercice 10
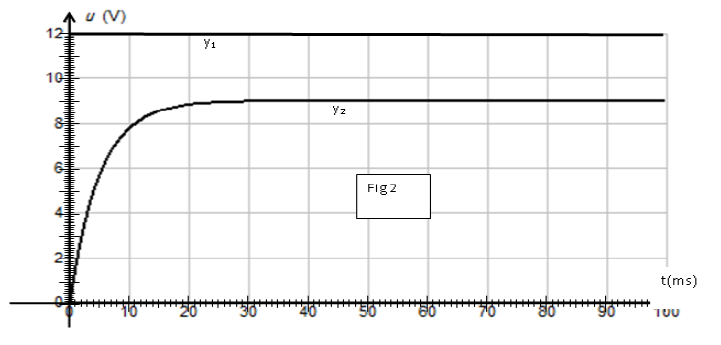
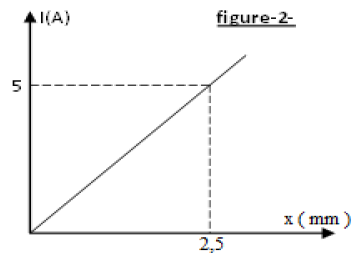
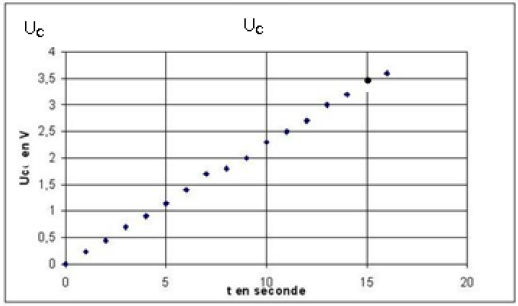
Etoile Vega et son spectre L'étoile Véga se trouve dans la constellation de la Lyre. Elle émet de la lumière que l'on
peut décomposer. On obtient un spectre dont voici sa représentation :
La première raie à $x = 0 cm$ correspond à la longueur d'onde $λ=400nm$ et la dernière raie
correspondant à $x=8,5 cm$ est la longueur d'onde $λ=700nm$.
A chaque raie correspond une abscisse $x$ sur l‟axe orienté. La longueur d'onde $λ$ est fonction
affine de $x$ de la forme $λ = ax +b$.
1°/Quelle est la nature du spectre ?
2°/En déduire si l'étoile possède une atmosphère.
3°/Tracer, rapidement, avec seulement $2$ points, $λ$ en fonction de $x$.
4°/En déduire le coefficient directeur de la droite ainsi que son ordonnée à l'origine.
Donner alors l'équation numérique de $λ = ax +b$
5°/A l'aide de l'équation numérique trouver les valeurs des longueurs d'onde émises par l'étoile.
6°/Y-a-t-il de l'hydrogène ou de l'hélium dans l'étoile Véga ? Conclure. Données :
-longueurs d'onde en nm émise par l'élément $H : 398 – 410 – 434-486$
-longueurs d'onde en $nm$ émise par l'élément $He : 380 – 403 – 414-447$
Exercice 11
On donne les spectres de deux éléments, le titane et le nickel, ainsi que le spectre d'une étoile.
Ces spectres ont été réalisés dans les mêmes conditions et les réglages du spectroscope étaient les mêmes.
1) Quel nom donne-t-on aux spectres des deux éléments ?
2) Expliquer l'allure du spectre de l'étoile en utilisant les mots ou les expressions suivantes :
spectre (ou fond) continu ; raies d'absorption.
3) La comparaison du spectre de l'étoile et des spectres de chaque élément permet de faire
uneaffirmation relative à la composition chimique de l'étoile. Laquelle ?




Exercice1
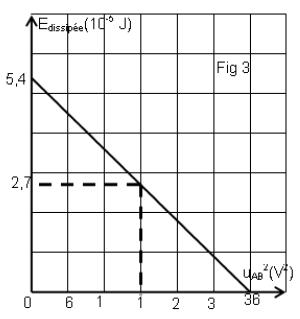
Deux fentes $F_{1}$ et $F_{2}$ distantes de $a=2mm$ émettent de la lumière provenant d'une
même fente $F$ Elles produisent un système d'interférences lumineuses sur un écran placé à la
distance $D=2m$ des fentes. La lumière de la source $F$ contient deux radiations
monochromatiques, de longueur d‟onde $λ_{1}=0,60µm$ et $λ_{2}=0,48µm$. L'interfrange $i$ (distance
séparant les milieux de deux franges sombres ou de deux brillantes consécutive) est lié à $λ$ par
la relation $i=λ\frac{D}{a}$
1. Représenter à l'échelle $5$, sur une largeur de $15cm$ :
a) la figure d'interférences obtenue avec la radiation de longueur d'onde $λ_{1}$
b) la figure d‟interférences obtenue avec la radiation de longueur d'onde $λ_{2}$
c) la figure d‟interférences obtenue avec la lumièreémise par la source $F$
2. Qu'observerait –on si la source Fémettait de la lumière blanche
Exercice 2
A l'aide d'un dispositif interférentiel, on crée deux sources lumineuses $S_{1}$ et $S_{2}$ synchrones et
cohérentes distantes de a. quand le dispositif est éclairé par une source de lumière
monochromatique de longueur d'onde $λ=0,6µm$, on observe des franges d'interférence sur
l'écran $E$ placé à$ D=2,5m$ de $S_{1}$ et $S_{2}$
1. Etablir l'expression de la différence de marche au point $M$ de l'écran
2. Déterminer la distance entre les deux sources pour que la distance entre les milieux de la $6^{e}$
et $9^{e}$ frange brillante située de part et d'autre de la frange centrale numérotée $0$ soit égale à
$1,5cm$
3. Déterminer la nature de la frange en un point $P$ de $E$ distant de $2,5mm$ de la frange centrale
Exercice 3
Deux fentes $F_{1}$ et $F_{2}$ sont éclairées par une fente source en lumière monochromatique rouge de
longueur d'onde $λ=0,64µm$ et se comportent comme deux sources synchrones et en phase. La
figure d'interférence est observée sur un écran. On considère un point $M$ sur un écran situé à
la distanced1 de $F_{1}$ et $d_{2}$ de $F_{2}$ ('schéma)
1. Les vibrations lumineuses issues des fentes $F_{1}$ et $F_{2}$ sont-elles ? Sont –elles en phase
(Justifier les réponses)
2. La vibration lumineuse émise par la fente $F_{1}$ arrive en $M$ avec un certain retard .Exprimer
ce retard en fonction de d1et de la vitesse $c$ de la lumière dans l'air
3. Même question pour la vibration lumineuse issue de la fente $F_{2}$
4. En déduire à quelles conditions le point $M$ sera sur frange brillante ; sur une frange
sombre$5$. Que peut-on dire des points $M$ suivants :
-$M$ est tel que $d_{2}-d_{1}=0$
-$M$ est tel que $d_{2}-d_{1}= 3,20 µm$
-M est tel que $d_{2}-d_{1}=2,24 µm$
Exercice 4
La lumière serait de nature contradictoire. Si une théorie permet d'expliquer de nombreux
phénomènes, elle peut s'avérer insuffisante pour en comprendre d'autres.
Le but de cet exercice est de montrer que, selon l'expérience réalisée, un des aspects
du comportement de la lumière. $A$ cet effet on réalise le dispositif ci-après :
1. Dispositif expérimental.
$(S)$ est une source de lumière qui éclaire 
deux fentes fines, verticales distantes de $a =
1,5 mm$. La source $(S)$ est équidistante des
deux fentes. $(E)$ est un écran opaque vertical
placé à une distance $D = 2 m$ du plan des
fentes.
a) Quel phénomène se produit à la sortie
de chaque fente ? Quel aspect de la lumière
permet-il de mettre en évidence ?
b) Justifier l'utilisation d'une source unique pour éclairer les deux dentes.
c) Reproduire le schéma et représenter la marche des faisceaux lumineux issus des fentes $F_{1}$
et $F_{2}$. Hachurer le champ où l'on peut observer le phénomène d'interférence.
2. La source $(S)$ émet une lumière monochromatique de longueur d'onde $λ$.
a) Qu'observe-t-on sur l'écran ? Préciser la direction des franges et la nature de la frange
centrale qui se forme en $O$.
b) Pour déterminer la longueur d'onde $λ$, on compte $5$ franges brillantes de part et d'autres de
la frange centrale occupant ensemble une largeur $l = 8 mm$. En déduire la valeur de $λ$.
3. La source précédente $(S)$ est remplacée par une source $(S')$ qui émet simultanément deux
radiations monochromatiques de longueur d'onde $λ_{1} = 0,60 µm$, et $λ_{2} = 0,54 µm$. Il se produit
une superposition des systèmes de franges formées par les deux radiations.
A quelle distance $x$ du point $O$ se produit la première coïncidence de franges brillantes ?
Exercice5
Un pinceau de lumière monochromatique émis par un laser hélium-néon éclaire deux fentes
parallèles séparées par une distance $a =0,5mm$ . Un écran est placé perpendiculairement au
pinceau lumineuxàunedistance $D=2m$ duplandes fentes. Dessinerle dispositif expérimental.
1. Interpréterlaformationdesfrangesbrillantesetobscures.
2. Définir et calculer la différence de marche aux $2$ fentes d'un point $M$ de l'écran, pour en
déduirelapositiondesfrangesbrillanteset obscures
3. Préciser la nature de la frange centrale appartenant au plan médiateur des $2$ fentes.
4. Définir et calculer l'interfrange. Quelle est l'influence des différents paramètres sur
l'interfrange ? Comment doit-on modifier la distance entre les $2$ fentes pour obtenir des
frangesplusespacées ?
5. Calculer la longueur d'onde et la fréquence de la lumière émise par le laser, sachant que $6$
frangessontespacéesde$12,7mm$.
6. Est-ce que la longueur d'onde ou la fréquence change (ou aucune des deux), si le rayon
lumineux se propage dans le verre ? Calculer les nouvelles valeurs. (On sait que dans le verre
lacéléritédelalumièrevaut$200000km/s$.
Exercice6
Une lumière monochromatique, issue d‟une fente $F$, tombe sur un écran $E$ percé de deux
fentes $F_{1}$ et $F_{2}$ parallèleà $F$. Un dispositif spécial permet de faire varier la distance entre les
fentes$F_{1}$ et $F_{2}(F_{1}F_{2}=a$)quirestetoutefoissituéeàégaledistancede$F$.
1. Ondisposeunécran$K$,parallèleàEetàunedistancedde celui-ci.Qu'observe-t-onsurl'écranK
2. La longueurd‟ondedelalumièremonochromatiqueest $λ$.
OnmesuredansleplanKl'intervalleLséparant$N$frangesbrillantesconsécutives.
Etablir la formule donnant a en fonction de $λ, N, d$ et $L$ (On supposera établie la formule de
l'interfrange) Calculer a lorsque $λ=0,55µm, L=7,2mm, N=7$ et $d=1,20m$
3. On augmente l'intervalle $a =F_{1}F_{2}$
Qu''en résulte-il sur le phénomène observé sur l'écran ?
D'autre part on remarque que pour un interfrange inférieur à $0,2mm$, l'observation du
phénomène devient très difficile à l'œil nu .Quelle sera la valeur limite $a'$ de la distance $F_{1}F_{2}$
séparant les deux fentes ?
4. Combien observe-t-on de franges brillantes sur l'intervalle $L=7,2mm$ de l'écran $K$ quand
$a=a'$? La mesure de l'intervalle est faite à partir d'une frange brillante
Exercice7
1. Soit à la distance de deux fentes fines et parallèles $F$ et $F'$ dans l'expérience de Young. On
éclaire $F$ et $F'$ par une fente lumineuse parallèle aux précédentes et à égale distance de chacune
d'elle. Soit $λ$ la longueur d'onde dans le vide de la lumière monochromatiqueemployée. On
observe dans l'air des franges d'interférences sur un écran $(P)$ parallèle au plan des deux
fentes et situé à une distance $d$ de ces fentes. Soit la largeur de $N$ interfranges consécutifs (on
prendra comme plan de figure un plan perpendiculaire au plan $(F F'))$
1.1. Etablir la relation donnant $λ$ en fonction de $a,d,l$ et $N$.
A N :$a=2,00mm ;l=4,00mm ; N=12$et $d=1,00m$. Calculer $λ$
1.2. Quelle serait la nouvelle longueur $l$ du même nombre $N $ d'interfranges si tout le dispositif
était plongé dans un milieu d'indice par rapport à l'air
A.N :$n_{o}=1,30$
1.3. Le système étant placé dans l'air,on recouvre la fente $F$ du côté de l'écran par un verre à
faces parallèles d'épaisseur e et d'indice $n=1,52$ .Qu'observe-t-on sur l'écran.
Expliquer le phénomène. Calculer e si le déplacement de la frange centrale est $X=4,40mm$
1.4. On place sur $F$ une autre lame d'épaisseur $e'$ et d'indice $n'$ ; Le système de franges
obtenu est alors identique à celui réalisé avant la mise en place des deux lames .Donner en
fonction de $e, n$ et $n'$ l'expression de $e'$
Calculer $e'$ si $n'=1,402$.Le dispositif est celui de la question.1, mais la source émet deux
radiations : $λ=0,550 µm$ et $λ = 0,650 µm$.
On observe simultanément les deux franges. Déterminer dans le plan$(P)$, la plus petite
distance par rapport à la frange centrale où les milieux de deux franges brillantes
correspondant aux deux radiations coïncident.
Exercice8
La source $F$ n'est plus monochromatique, mais des filtres permettent d'obtenir des
radiations monochromatiques différentes (voir figure). Pour chaque radiation, on mesure la
longueur d'onde correspondant à $6$ interfranges $i (i$ est la distance séparant le milieu de deux
franges brillantes consécutives ou de deux franges sombres consécutives) (voir figure).
1. Pourquoi mesure-t-on la distance correspondant à $6$ interfranges plutôt que celle mesurant $1$
interfrange ?
2. On a obtenu les résultats suivants. Compléter le tableau.
Couleur
| Couleur | |||||
| $6i$ | $14,1$ | $15,6$ | $17,4$ | $18,3$ | $19,5$ |
| $λ (µm)$ | $0,47$ | $0,52$ | $0,58$ | $0,61$ | $0,65$ |
3. Tracer la courbe représentative de la fonction $i=f(λ)$ .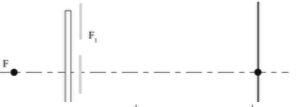
4. La relation $i=λ\frac{D}{a}$ est-elle en accord
avec la courbe obtenue précédemment ?
5. Comment faudrait-il modifier le
dispositif expérimental pour obtenir des mesures
avec une plus grande précision ?
6. Quelle serait la valeur de l'interfrange obtenu
avec une radiation de longueur d'onde $0,50μm$ ?
7. Ondisposed‟une source monochromatique de
longueur d'onde inconnue. Comment feriez-
vousexpérimentalementpourladéterminer.
Exercice 9
On réalise une expérience d'interférences lumineuses avec le dispositif d'Young, en utilisant
une lumière monochromatique de longueur d'onde $λ_{1} = 0,52 μm$. La fente-source $F$ éclaire
deux fentes fines identiques $F_{1}$ et $F_{2}$ situées dans un plan vertical et distantes de $F_{1}F_{2} = a =2mm$
.Un écran d'observation $(E)$ est placé à $150 cm$ du plan contenant $F_{1}$ et $F_{2}$
et parallèlement à celui-ci.
1. a- Décrire et expliquer le phénomène observé sur l'écran $(E)$.
b-Quelle conclusion peut-on en tirer quant à la nature de la lumière ?
2. Définir et calculer l'interfrange $i$.
3. La frange centrale brillante est d'ordre zéro.
Calculer la distance séparant la troisième frange brillante à gauche de la frange centrale
et la deuxième frange noire à droite de cette frange centrale.
La fente-source $F$ émet maintenant une radiation monochromatique de longueur d'onde
$λ_{2} = 0,65μm$.
4. A quelle distance de cette fente-source $F$ doit-on placer l'écran d'observation $(E)$ pour que
l'nterfrange $i'$ obtenu avec ce dispositif soit égal à l'interfrange $i$ de la question $2$ ? La
distance entre la fente-source $F$ et le plan contenant $F_{1}$ et $F_{2}$ est égale à $50 cm$.
5. La fente-source $F$ émet simultanément les deux radiations de longueurs d'onde
$λ_{1}= 0,52 μm$ et $λ_{2}= 0,65 μm$.
On remet l'écran $(E)$ à la position où il est distant de $150 cm$ du plan contenant $λ_{2}= 0,65 μm$.
On remet l'écran $(E)$ à la position où il est distant de $150 cm$ du plan contenant $F_{1}$ et $F_{2}$.
6. A quelle distance de la frange centrale aura lieu la première coïncidence des franges
brillantes des deux systèmes de franges obtenus.
Exercice10
Le dispositif des fontes d'YOUNG schématisé sur la figure -1 permet de réaliser une
expérience de mise en évidence d'interférences lumineuses. La source $(S)$ émet une
lumière monochromatique delongueur d'onde $λ=0,6.10^{-6} m(P)$ est un
plan opaque comportant deux fentes fines
$S_{1}$ et $S_{2}$ distantes de $a = 1mm$ et 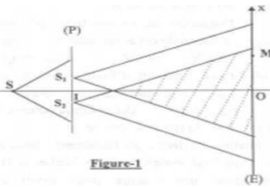
assimilables à deux sources ponctuelles
monochromatique symétriques par
rapport à un point $I$ milieu de $S_{1}S_{2}$.Un
écran $(E)$ est disposé parallèlement à $(P)$
et à une distance $D = 2 m$ de celui-ci.
On observe des interférences lumineuses
dans la représenté hachurée sur le schéma
où les deux faisceaux issus de $S_{1}$ et $S_{2}$
couvrent une partie commune. L'intersection de cette zone hachurée avec l'écran $(E)$ est un
ensemble de franges brillantes équidistantes ayant la couleur de lumière monochromatique.
Deux franges brillantessuccessives sont séparées par une frange sombre, et la frange centrale
en $O$ est brillante. Un point$ M$ du champ d'interférence est repéré par son abscisse $x=
OM$ Lorsque $M$ appartient à une frange brillante, ilvérifielarelation$MS_{2}-MS_{1}=kλ$ (aveckentier).
Par contre s'il appartient à une frange sombre il vérifie la relation $MS_{2}- MS_{1}= (2k+1)\frac{λ}{2}$
(aveckentier).
1) a -Montrer que la différence de marche a pour expression $(MS_{2}- MS_{1}) =\frac{ax}{D}$
b -En déduire l'expression de l'abscisse $x$ d'un point $M$ de l'écran en fonction de $λ, D$ et $ a $:
- Lorsqu'ilappartientàunefrange brillante
-Lorsqu'ilappartientàunefrangesombre.
2) a -Déterminer l'expression de l'interfrange $i$ en fonction de $λ, D$ et
a. Calculer $i$.
b -Préciser, en le justifiant, la nature (brillante ou sombre) de la frange d'abscisse $x = - 4,2 mm$.
3) Onapporteleschangementssuivantsaudispositif expérimental de la figure $-1$ :
-on supprime la source $(S)$ et le plan opaque $(P)$- à l'emplacement des deux sources
secondaires $S_{1}$ et $S_{2}$ on dispose de deux sources $S'_{1}$et $S'_{2}$ totalement indépendantes, émettant
chacune la lumière monochromatique de longueur
d'onde $l = 0,6.10^{-6}m$. (figure -2) on n'observe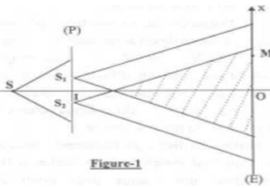
d'interférences lumineuses. Expliquer pourquoi ?
4) Citer un dispositif, autre que les fentes
d'YOUNG, permettant de réaliser
une expérience de mise en évidence
d'interférences lumineuses :
- on tracera la marche des rayons lumineux
- et on hachurera la zone où les deux
faisceaux lumineux, issus des deux sources
secondaires, couvrent une partie commune
correspondant aux interférences lumineuse.